题目内容
下表给出了代数式-x2+bx+c与x的一些对应值:
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=-x2+bx+c,直接写出0≤x≤2时y的最大值.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| -x2+bx+c | … | 5 | n | c | 2 | -3 | -10 | … |
(2)设y=-x2+bx+c,直接写出0≤x≤2时y的最大值.
考点:待定系数法求二次函数解析式,二次函数的最值
专题:计算题
分析:(1)把(-2,0)、(1,2)分别代入-x2+bx+c中得到关于b、c的方程组,然后解方程组即可得到b、c的值;然后计算x=-1时的代数式的值即可得到n的值;
(2)利用表中数据求解.
(2)利用表中数据求解.
解答:解:(1)根据表格数据可得
,解得
,
∴-x2+bx+c=-x2-2x+5,
当x=-1时,-x2-2x+5=6,即n=6;
(2)根据表中数据得当0≤x≤2时,y的最大值是5.
|
|
∴-x2+bx+c=-x2-2x+5,
当x=-1时,-x2-2x+5=6,即n=6;
(2)根据表中数据得当0≤x≤2时,y的最大值是5.
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
某县为发展教育事业,加强了对教育经费的投入,2012年投入3000万元,预计2014年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
| A、3000x2=5000 |
| B、3000(1+x)2=5000 |
| C、3000(1+x%)2=5000 |
| D、3000(1+x)+3000(1+x)2=5000 |
掷一枚均匀的骰子,前5次朝上的点数恰好是1~5,则第6次朝上的点数( )
| A、一定是6 |
| B、是6的可能性大于是1~5中的任意一个数的可能性 |
| C、一定不是6 |
| D、是6的可能性等于是1~5中的任意一个数的可能性 |
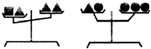 设“▲”、“■”和“●”分别表示三种不同的物体,现用同一天平秤两次,
设“▲”、“■”和“●”分别表示三种不同的物体,现用同一天平秤两次,如图,那么▲、■、●三种物质按质量从小到大排列应该是( )
| A、■●▲ | B、▲■● |
| C、■▲● | D、●▲■ |
 在△ABC中,AB=AC=10,BD是AC边上的高,DC=2,则BD等于( )
在△ABC中,AB=AC=10,BD是AC边上的高,DC=2,则BD等于( )A、2
| ||
| B、4 | ||
| C、6 | ||
| D、8 |
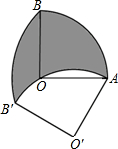 如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB′上时,n为
如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB′上时,n为



 作图:在数轴上找到表示实数-
作图:在数轴上找到表示实数-