题目内容
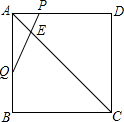 如图,正方形ABCD中,点P为边AD上一点,DP=3AP,点Q为边AB的中点,连接PQ交对角线AC于点E.试求
如图,正方形ABCD中,点P为边AD上一点,DP=3AP,点Q为边AB的中点,连接PQ交对角线AC于点E.试求| PE |
| EQ |
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:如图,作辅助线;设AP=λ,得到DP=3AP=3λ;求出QF的长度,这是解决该问题的关键;运用△APE∽△FQE,列出比例式即可解决问题.
解答: 解:如图,过点Q作QF∥BC,交AC于点F;
解:如图,过点Q作QF∥BC,交AC于点F;
设AP=λ,则DP=3AP=3λ;
∵四边形ABCD为正方形,且Q为AB的中点,
∴BC=AB=AD=4λ,AQ=2λ;AD∥BC;
∴AP∥QF;
∴△AQF∽△ABC,△APE∽△FQE,
∴QF:BC=AQ:AB,PE:QE=AP:QF①,
∵BC=AB=4λ,AQ=2λ,
∴QF=2λ,代入①得:PE:QE=1:2,
即
的值为
.
 解:如图,过点Q作QF∥BC,交AC于点F;
解:如图,过点Q作QF∥BC,交AC于点F;设AP=λ,则DP=3AP=3λ;
∵四边形ABCD为正方形,且Q为AB的中点,
∴BC=AB=AD=4λ,AQ=2λ;AD∥BC;
∴AP∥QF;
∴△AQF∽△ABC,△APE∽△FQE,
∴QF:BC=AQ:AB,PE:QE=AP:QF①,
∵BC=AB=4λ,AQ=2λ,
∴QF=2λ,代入①得:PE:QE=1:2,
即
| PE |
| EQ |
| 1 |
| 2 |
点评:该题主要考查了正方形的性质、相似三角形的判定及其性质等几何知识点的应用问题;作辅助线构造相似三角形是解题的关键.

练习册系列答案
相关题目

 如图,直线L:与x轴、y轴分别交于A(4,0)、B(0,2)两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:与x轴、y轴分别交于A(4,0)、B(0,2)两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.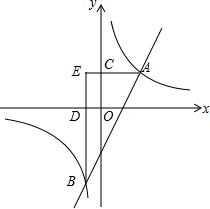 如图,双曲线y=
如图,双曲线y=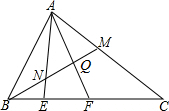 如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC,求BN:NQ:QM的值.
如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC,求BN:NQ:QM的值. 如图所示,点D、E分别在AB、AC上,F为AB上一点,延长FE交BC的延长线于G,∠ECG=∠A+∠ADE,求证:DE∥BC.
如图所示,点D、E分别在AB、AC上,F为AB上一点,延长FE交BC的延长线于G,∠ECG=∠A+∠ADE,求证:DE∥BC.