题目内容
 如图,直线L:与x轴、y轴分别交于A(4,0)、B(0,2)两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:与x轴、y轴分别交于A(4,0)、B(0,2)两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.(1)求直线L的解析式;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t何值时△COM≌△AOB,并求此时M点的坐标.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得函数解析式;
(2)根据速度乘以时间等于路程,可得AM的长,根据线段的和差,可得OM的长,根据三角形的面积公式,可得答案;
(3)根据全等三角形的性质,可得OM与OB的关系,根据OM的长,可得M点的坐标,根据线段的和差,可得AM的长根据AM的长,可得t值.
(2)根据速度乘以时间等于路程,可得AM的长,根据线段的和差,可得OM的长,根据三角形的面积公式,可得答案;
(3)根据全等三角形的性质,可得OM与OB的关系,根据OM的长,可得M点的坐标,根据线段的和差,可得AM的长根据AM的长,可得t值.
解答:解:(1)设直线L的解析式为y=kx+b,
由直线L:与x轴、y轴分别交于A(4,0)、B(0,2)两点,得
,
解得
.
直线L的解析式为y=-
x+2;
(2)由动点M从A点以每秒1个单位的速度沿x轴向左移动,t秒运动了t个单位,
即AM=t.
①当0≤t<4时,由线段的和差得OM=4-t,
△COM的面积S与M的移动时间t之间的函数关系式S=
OM•OC=
×4(4-t)=8-2t;
②当t>4时,由线段的和差得OM=t-4,
△COM的面积S与M的移动时间t之间的函数关系式S=
OM•OC=
×4(t-4)=2t-8,
综上所述:S=
;
(3)由△COM≌△AOB,得
OM=0B=2,即M(2,0)或(-2,0).
①当OM=2时AM=OA-OM=4-2,即M行驶了2秒;
②当OM=-2时,AM=AO-OM=4-(-2)=6,即M行驶了6秒,
综上所述:当t=2时,△COM≌△AOB,此时M点的坐标(2,0);
当t=6时,△COM≌△AOB,此时M点的坐标(-2,0).
由直线L:与x轴、y轴分别交于A(4,0)、B(0,2)两点,得
|
解得
|
直线L的解析式为y=-
| 1 |
| 2 |
(2)由动点M从A点以每秒1个单位的速度沿x轴向左移动,t秒运动了t个单位,
即AM=t.
①当0≤t<4时,由线段的和差得OM=4-t,
△COM的面积S与M的移动时间t之间的函数关系式S=
| 1 |
| 2 |
| 1 |
| 2 |
②当t>4时,由线段的和差得OM=t-4,
△COM的面积S与M的移动时间t之间的函数关系式S=
| 1 |
| 2 |
| 1 |
| 2 |
综上所述:S=
|
(3)由△COM≌△AOB,得
OM=0B=2,即M(2,0)或(-2,0).
①当OM=2时AM=OA-OM=4-2,即M行驶了2秒;
②当OM=-2时,AM=AO-OM=4-(-2)=6,即M行驶了6秒,
综上所述:当t=2时,△COM≌△AOB,此时M点的坐标(2,0);
当t=6时,△COM≌△AOB,此时M点的坐标(-2,0).
点评:本题考查了一次函数的综合题,利用了待定系数法求解析式,(2)分类讨论是解题关键,根据三角形的面积公式得出函数解析式,(3)利用了全等三角形的性质.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
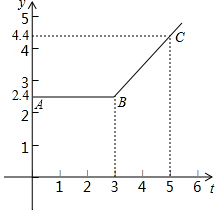 图中的折线ABC为从甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(分钟)之间变化关系的图象.
图中的折线ABC为从甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(分钟)之间变化关系的图象.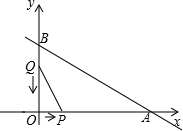 如图,在平面直角坐标系中,OA=12cm,OB=6cm,点P从点O开始沿OA向点A移动,点Q从点B开始沿BO向点O移动,点P、Q的移动速度都是1cm/s,如果点P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么
如图,在平面直角坐标系中,OA=12cm,OB=6cm,点P从点O开始沿OA向点A移动,点Q从点B开始沿BO向点O移动,点P、Q的移动速度都是1cm/s,如果点P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么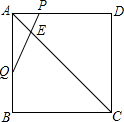 如图,正方形ABCD中,点P为边AD上一点,DP=3AP,点Q为边AB的中点,连接PQ交对角线AC于点E.试求
如图,正方形ABCD中,点P为边AD上一点,DP=3AP,点Q为边AB的中点,连接PQ交对角线AC于点E.试求