题目内容
8.(1)对于任意自然数n,代数式n(n+3)-(n-4)(n-5)的值都能被4整除吗?请说明理由.(2)小明在做一个多项式除以$\frac{1}{2}$a的题时,由于粗心误以为乘以$\frac{1}{2}$a,结果是8a4b-4a3+2a2,那么你能知道正确的结果是多少吗?
分析 (1)将原式展开化简可得4(3n-5),根据n是自然数可知原式能被4整除;
(2)先根据误乘的结果用除法求出原多项式,再用该多项式除以$\frac{1}{2}$a可得结果.
解答 解:(1)能,
原式=n2+3n-(n2-5n-4n+20)
=n2+3n-n2+5n+4n-20
=12n-20
=4(3n-5),
因为n是自然数,所以3n-5是整数,
因此原式能被4整除;
(2)根据题意,原多项式为(8a4b-4a3+2a2)÷$\frac{1}{2}$a=16a3b-8a2+4a.
故正确结果为:(16a3b-8a2+4a)÷$\frac{1}{2}$a=32a2b-16a+8.
点评 本题主要考查整式的运算能力,熟练掌握多项式与单项式相乘、除,多项式与多项式相乘的运算法则是关键也是基础.

练习册系列答案
相关题目
17.如图,是一组按照某种规律摆放成的图案,则图10中三角形的个数是( )


| A. | 100 | B. | 66 | C. | 36 | D. | 32 |
18. 如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
 如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )| A. | 2.5cm | B. | 3cm | C. | 4cm | D. | 5cm |
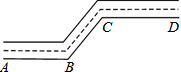 如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=150°,当街道AB和CD平行时,∠BCD=150度,根据是两直线平行,内错角相等.
如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=150°,当街道AB和CD平行时,∠BCD=150度,根据是两直线平行,内错角相等.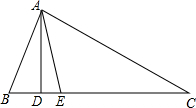 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求: