题目内容
 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.(1)求证:CD为⊙O的切线.
(2)若
| CD |
| AD |
| 3 |
| 4 |
考点:切线的判定,角平分线的性质,勾股定理,解直角三角形
专题:几何综合题
分析:(1)连接OC,推出∠DAC=∠CAB,∠OAC=∠OCA,求出∠DAC=∠OCA,得出OC∥AD,推出OC⊥DC,根据切线的判定判断即可;
(2)连接BC,可证明△ACD∽△ABC,得出比例式,求出BC,求出圆的直径AB,再根据勾股定理得出CE,即可求出答案.
(2)连接BC,可证明△ACD∽△ABC,得出比例式,求出BC,求出圆的直径AB,再根据勾股定理得出CE,即可求出答案.
解答: (1)证明:连接OC,
(1)证明:连接OC,
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∵OC为⊙O半径,
∴CD是⊙O的切线;
 (2)解:连接BC,
(2)解:连接BC,
∵AB为直径,
∴∠ACB=90°,
∵AC平分∠BAD,
∴∠CAD=∠CAB,
∵
=
,
∴令CD=3,AD=4,得AC=5,
∴
=
,
=
,
∴BC=
,
由勾股定理得AB=
,
∴OC=
,
∵OC∥AD,
∴
=
,
∴
=
,
解得AE=
,
∴cos∠DAB=
=
=
.
 (1)证明:连接OC,
(1)证明:连接OC,∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∵OC为⊙O半径,
∴CD是⊙O的切线;
 (2)解:连接BC,
(2)解:连接BC,∵AB为直径,
∴∠ACB=90°,
∵AC平分∠BAD,
∴∠CAD=∠CAB,
∵
| CD |
| AD |
| 3 |
| 4 |
∴令CD=3,AD=4,得AC=5,
∴
| BC |
| AC |
| 3 |
| 4 |
| BC |
| 5 |
| 3 |
| 4 |
∴BC=
| 15 |
| 4 |
由勾股定理得AB=
| 25 |
| 4 |
∴OC=
| 25 |
| 8 |
∵OC∥AD,
∴
| OC |
| AD |
| OE |
| AE |
∴
| ||
| 4 |
AE-
| ||
| AE |
解得AE=
| 100 |
| 7 |
∴cos∠DAB=
| AD |
| AE |
| 4 | ||
|
| 7 |
| 25 |
点评:本题考查了切线的判定以及角平分线的定义、勾股定理和解直角三角形,是中学阶段的重点内容.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.下列结论正确的是( )
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.下列结论正确的是( )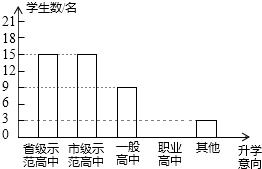 近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表:
近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表: 给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
 如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠AEF=
如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠AEF=