题目内容
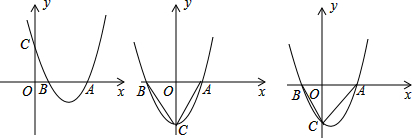
在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.
(1)若m=2,n=1,求A、B两点的坐标;
(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,-1),求∠ACB的大小;
(3)若m=2,△ABC是等腰三角形,求n的值.
(1)若m=2,n=1,求A、B两点的坐标;
(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,-1),求∠ACB的大小;
(3)若m=2,△ABC是等腰三角形,求n的值.

考点:二次函数综合题
专题:压轴题
分析:(1)已知m,n的值,即已知抛物线解析式,求解y=0时的解即可.此时y=x2-(m+n)x+mn=(x-m)(x-n),所以也可直接求出方程的解,再代入m,n的值,推荐此方式,因为后问用到的可能性比较大.
(2)求∠ACB,我们只能考虑讨论三角形ABC的形状来判断,所以利用条件易得-1=mn,进而可以用m来表示A、B点的坐标,又C已知,则易得AB、BC、AC边长.讨论即可.
(3)△ABC是等腰三角形,即有三种情形,AB=AC,AB=BC,AC=BC.由(2)我们可以用n表示出其三边长,则分别考虑列方程求解n即可.
(2)求∠ACB,我们只能考虑讨论三角形ABC的形状来判断,所以利用条件易得-1=mn,进而可以用m来表示A、B点的坐标,又C已知,则易得AB、BC、AC边长.讨论即可.
(3)△ABC是等腰三角形,即有三种情形,AB=AC,AB=BC,AC=BC.由(2)我们可以用n表示出其三边长,则分别考虑列方程求解n即可.
解答:解:(1)∵y=x2-(m+n)x+mn=(x-m)(x-n),
∴x=m或x=n时,y都为0,
∵m>n,且点A位于点B的右侧,
∴A(m,0),B(n,0).
∵m=2,n=1,
∴A(2,0),B(1,0).
(2)∵抛物线y=x2-(m+n)x+mn(m>n)过C(0,-1),
∴-1=mn,
∴n=-
,
∵B(n,0),
∴B(-
,0).
∵AO=m,BO=
,CO=1
∴AC=
=
,
BC=
=
,
AB=AO+BO=m+
,
∵(m+
)2=(
)2+(
)2,
∴AB2=AC2+BC2,
∴∠ACB=90°.
(3)∵A(m,0),B(n,0),C(0,mn),且m=2,
∴A(2,0),B(n,0),C(0,2n).
∴AO=2,BO=|n|,CO=|2n|,
∴AC=
=2
,
BC=
=
|n|,
AB=xA-xB=2-n.
①当AC=BC时,2
=
|n|,解得n=2(A、B两点重合,舍去)或n=-2;
②当AC=AB时,2
=2-n,解得n=0(B、C两点重合,舍去)或n=-
;
③当BC=AB时,
|n|=2-n,
当n>0时,
n=2-n,解得n=
,
当n<0时,-
n=2-n,解得n=-
.
综上所述,n=-2,-
,-
,
时,△ABC是等腰三角形.
∴x=m或x=n时,y都为0,
∵m>n,且点A位于点B的右侧,
∴A(m,0),B(n,0).
∵m=2,n=1,
∴A(2,0),B(1,0).
(2)∵抛物线y=x2-(m+n)x+mn(m>n)过C(0,-1),
∴-1=mn,
∴n=-
| 1 |
| m |
∵B(n,0),
∴B(-
| 1 |
| m |
∵AO=m,BO=
| 1 |
| m |
∴AC=
| AO2+OC2 |
| m2+1 |
BC=
| OB2+OC2 |
| ||
| m |
AB=AO+BO=m+
| 1 |
| m |
∵(m+
| 1 |
| m |
| m2+1 |
| ||
| m |
∴AB2=AC2+BC2,
∴∠ACB=90°.
(3)∵A(m,0),B(n,0),C(0,mn),且m=2,
∴A(2,0),B(n,0),C(0,2n).
∴AO=2,BO=|n|,CO=|2n|,
∴AC=
| AO2+OC2 |
| 1+n2 |
BC=
| OB2+OC2 |
| 5 |
AB=xA-xB=2-n.
①当AC=BC时,2
| 1+n2 |
| 5 |
②当AC=AB时,2
| 1+n2 |
| 4 |
| 3 |
③当BC=AB时,
| 5 |
当n>0时,
| 5 |
| ||
| 2 |
当n<0时,-
| 5 |
| ||
| 2 |
综上所述,n=-2,-
| 4 |
| 3 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查了因式分解、二次函数性质、利用勾股定理求点与点的距离、等腰三角形等常规知识,总体难度适中,是一道非常值得学生加强练习的题目.

练习册系列答案
相关题目

 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E. 已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.
已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.