题目内容
7.把一根长为40cm的铁丝剪成两段,并把每一段围成一个正方形,要使这两个正方形的面积之和等于58cm2,该怎么剪?分析 设剪成的较短的这段为xcm,较长的这段就为(40-x)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于58cm2建立方程求出其解即可.
解答 解:设剪成的较短的这段为xcm,较长的这段就为(40-x)cm,由题意,得
($\frac{x}{4}$)2+($\frac{40-x}{4}$)2=58,
解得:x1=12,x2=28,
当x=12时,较长的为40-12=28cm,
当x=28时,较长的为40-28=12<28(舍去)
故较短的这段为12cm,较长的这段就为28cm.
点评 本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答本题时找到等量关系建立方程和运用根的判别式是关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
15.用一段长为30m的篱笆围成一个一边靠墙(长度不限)的菜园ABCD,并在垂直于墙的一边留一个1m宽的门,则平行于墙的篱笆长为( )时,菜园面积最大.
| A. | 15m | B. | 16m | C. | 15.5m | D. | 14m |
18.下列运算正确的是( )
| A. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | B. | $\sqrt{8}$=4$\sqrt{2}$ | C. | $\sqrt{3}$•$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
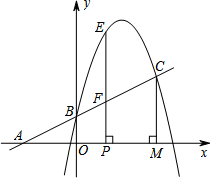 如图,已知直线y1=$\frac{1}{2}$x+b和抛物线y2=-$\frac{5}{4}$x2+ax+b都经过点B(0,1)和点C,过点C作CM⊥x轴于点M,且CM=$\frac{5}{2}$.
如图,已知直线y1=$\frac{1}{2}$x+b和抛物线y2=-$\frac{5}{4}$x2+ax+b都经过点B(0,1)和点C,过点C作CM⊥x轴于点M,且CM=$\frac{5}{2}$.