Question

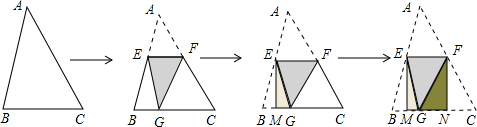
17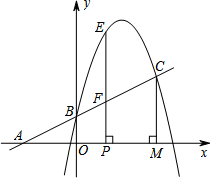．如图，已知直线y₁=$\frac{1}{2}$x+b和抛物线y₂=-$\frac{5}{4}$x²+ax+b都经过点B（0，1）和点C，过点C作CM⊥x轴于点M，且CM=$\frac{5}{2}$．
（1）求出抛物线的解析式；
（2）动点P从点O出发，以每秒1个单位长度的速度，沿OM向点M运动，过点P作PE⊥x轴分别交抛物线和直线于点E，F．当点P运动多少秒时，四边形EFMC为菱形？
（3）在（2）的条件下，在直线AC上确定一点Q，使得以点E、F、Q为顶点的三角形与△AMC相似，并求出点Q的坐标．

Answer 1

分析 （1）把点B的坐标代入y₁=$\frac{1}{2}$x+b，求得b=1，从而可得到直线的解析式为y₁=$\frac{1}{2}$x+1，把y=$\frac{5}{2}$代入y₁=$\frac{1}{2}$x+1，得x=3，从而求得点C（3，$\frac{5}{2}$），把B（0，1），C（3，$\frac{5}{2}$）代入y₂=-$\frac{5}{4}$x²+ax+b得到关于a，b的方程组，解得a、b的值，从而可求得抛物线的解析式；
（2）由菱形的性质可知：EF=FM=CM，设OP=t，则EF=EP-FP=-$\frac{5}{4}$t²+$\frac{15}{4}$t=$\frac{5}{2}$；FM=$\sqrt{\frac{5}{4}{t}^{2}-5t+10}$=$\frac{5}{2}$，从而可解得t的值；
（3）由（2）可知t=1，从而可求得点E、F的坐标，然后再求得点A的坐标：①过点过点E作，EQ₁⊥CF，可知：△EQ₁F∽△AMC，由菱形的性质可知点Q₁是CF的中点，从而可求得点Q₁的坐标；②过点E作EQ₂∥x轴，交直线BC与点Q₂，△EQ₂F∽△AMC，将y=4代入y₁=$\frac{1}{2}$x+1，得x=6，所以点Q₂的坐标为（6，4）．

解答 解：（1）把B（0，1）代入y₁=$\frac{1}{2}$x+b，得b=1，
∴y₁=$\frac{1}{2}$x+1，
把y=$\frac{5}{2}$代入y₁=$\frac{1}{2}$x+1，得x=3，
∴C（3，$\frac{5}{2}$），
把代B（0，1），C（3，$\frac{5}{2}$）代入y₂=-$\frac{5}{4}$x²+ax+b得
$\left\{\begin{array}{l}{b=1}\\{-\frac{45}{4}+3b+b=\frac{5}{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{b=1}\\{a=\frac{17}{4}}\end{array}\right.$
∴y₂=-$\frac{5}{4}$x²+$\frac{17}{4}$x+1．
（2）∵四边形EFMC为菱形，
则EF=FM=CM，
设OP=t，
则EF=EP-FP=-$\frac{5}{4}$t²+$\frac{17}{4}$t+1-（$\frac{1}{2}$t+1）=-$\frac{5}{4}$t²+$\frac{15}{4}$t；
FM=$\sqrt{P{F}^{2}+P{M}^{2}}$=$\sqrt{\frac{5}{4}{t}^{2}-5t+10}$；
∴-$\frac{5}{4}$t²+$\frac{15}{4}$t=$\frac{5}{2}$①；
$\sqrt{\frac{5}{4}{t}^{2}-5t+10}$=$\frac{5}{2}$②；
解①得：t=1或2
解②得：t=1或3
∴当点P运动1秒时，四边形EFMC为菱形；
（3）如图1所示：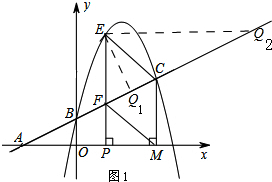

由（2）可知t=1，所以点F的横坐标为x=1，
将x=1代入y₁=$\frac{1}{2}$x+1，得y₁=$\frac{3}{2}$，将x=2代入y₂=-$\frac{5}{4}$x²+$\frac{17}{4}$x+1，得：y₂=4．
∴点E（1，4）、F（1，$\frac{3}{2}$），
将y=0代入y₁=$\frac{1}{2}$x+1，得x=-2，
∴点A的坐标为（-2，0）
①过点E作，EQ₁⊥CF，
∵四边形EFMC为菱形，
∴∠ECF=∠ACM，FE=FC．
∴∠EFC=∠ECF．
又∵∠EQ₁F=∠AMC=90°，
∴△EQ₁F∽△AMC．
∵EF=EC，EQ₁⊥FC，
∴FQ₁=CQ₁．
∵F（1，$\frac{3}{2}$），C（3，$\frac{5}{2}$），且点Q₁是CF的中点，
∴点Q₁的坐标为（2，2）；
②过点E作EQ₂∥x轴，交直线BC与点Q₂．
∵EQ₂∥x轴，
∴∠EQ₂F=∠CAM，∠Q₂EF=∠FPA=90°
∴∠Q₂EF=∠AMC=90°
∴△EQ₂F∽△AMC．
将y=4代入y₁=$\frac{1}{2}$x+1，得x=6，
∴点Q₂的坐标为（6，4）．
综上所述，点Q的坐标为（2，2）或（6，4）．

点评 本题主要考查的是二次函数、一次函数、菱形、相似三角形的综合应用，根据以点E、F、Q为顶点的三角形与△AMC相似，画符合题意的图形是解题的关键．