题目内容
9.抛物线y=$\frac{1}{2}$x2+3x+$\frac{5}{2}$上有两点(x1,y1)、(x2,y2).且x1<x2<-3,则y1与y2的大小关系是( )| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
分析 先求出抛物线的对称轴为直线x=-3,则可判断点(x1,y1)、(x2,y2)在对称轴左侧的抛物线上,然后根据二次函数的性质可判断y1与y2的大小.
解答 解:抛物线的对称轴为直线x=-$\frac{3}{2×\frac{1}{2}}$=-3,
而x1<x2<-3,
所以y1>y2.
故选B.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.

练习册系列答案
相关题目
19.已知∠α与∠β互余,∠β和∠γ互补,则∠γ的度数为( )
| A. | α | B. | β | C. | 90°+α | D. | 90°+β |
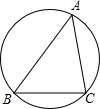 如图,在锐角三角形ABC中,BC=4,sinA=$\frac{4}{5}$,求三角形ABC外接圆的直径.
如图,在锐角三角形ABC中,BC=4,sinA=$\frac{4}{5}$,求三角形ABC外接圆的直径. 如图,直线AB,CD,EF被直线GH所截,如果CD∥AB,EF∥AB,CD与EF平行吗?为什么?
如图,直线AB,CD,EF被直线GH所截,如果CD∥AB,EF∥AB,CD与EF平行吗?为什么?