Question

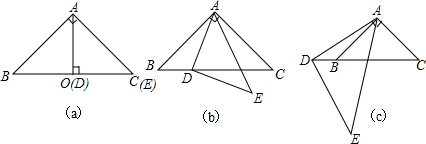
18．已知，△ABC中，∠BAC=90°，AB=AC，D是BC边上任一点，∠ADE=90°，AD=DE．
（1）如图（a）所示，当点D与BC边的中点O重合，点E与C重合时，$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$的值为1；
（2）如图（b）所示，当点D在BC边上运动时，$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$的值等于1，请填空并证明；
（3）如图（c）所示，当点D在CB的延长线上运动时，线段BD、CD、AE之间的数量关系是$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$=1（只写结论，不需证明）

Answer 1

分析 （1）根据中点的定义和勾股定理解答问题；
（2）如图（b），过点A作AM⊥BC于点M．构建直角△ABM、△ADM，设BM=x，BD=y，则BM=AM=MC=x，CD=2x-y，利用勾股定理得到BD²+CD²=AE²=4x²-4xy+2y²，易得到：$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$=1；
（3）解答过程同（2），结论同（1）、（2）．

解答 解：（1）∵点D是BC的中点，AB=AC，
∴AD⊥BC，BD=CD=AD，
∴BD²+CD²=CD²+AD²=AC²，即BD²+CD²=AE²，
∴$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$=1．
故答案是：1；

（2）如图（b），过点A作AM⊥BC于点M．
设BM=x，BD=y，则BM=AM=MC=x，CD=2x-y，
则BD²+CD²=y²+（2x-y）²=4x²-4xy+2y²．
∵AD²=AM²+DM²，DM=BM-BD=x-y，
∴AD²=x²+（x-y）²=2x²-2xy+y²．
又∵AE²=2AD²，
∴AE²=4x²-4xy+2y²．
∴BD²+CD²=AE²，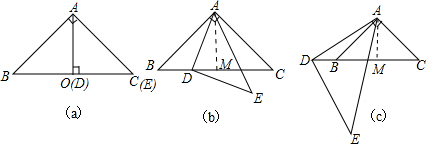
∴$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$=1．
故答案是：1；

（3）$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$=1
理由如下：如图（c），过点A作AM⊥BC于点M．
设BM=x，BD=y，则BM=AM=MC=x，CD=2x+y，
则BD²+CD²=y²+（2x+y）²=4x²+4xy+2y²．
∵AD²=AM²+DM²，DM=BM+BD=x+y，
∴AD²=x²+（x+y）²=2x²+2xy+y²．
又∵AE²=2AD²，
∴AE²=4x²+4xy+2y²．
∴BD²+CD²=AE²，
∴$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$=1．
故答案是：$\frac{B{D}^{2}+C{D}^{2}}{A{E}^{2}}$=1．

点评 本题考查了勾股定理，等腰直角三角形．解此类题目要注意将线段的问题转化成三角形的问题再进行计算．