题目内容
4.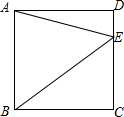 如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为2$\sqrt{13}$.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为2$\sqrt{13}$.
分析 根据正方形面积是△ABE面积的2倍,求出边长,再在Rt△BCE中利用勾股定理即可.
解答 解:设正方形边长为a,
∵S△ABE=18,
∴S正方形ABCD=2S△ABE=36,
∴a2=36,
∵a>0,
∴a=6,
在RT△BCE中,∵BC=6,CE=4,∠C=90°,
∴BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$.
故答案为2$\sqrt{13}$.
点评 本题考查正方形的性质、三角形的面积公式、勾股定理等知识,解题是关键是理解正方形面积是△ABE面积的2倍,属于中考常考题型.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
15.下列调查中,最适合用普查方式的是( )
| A. | 调查某品牌牛奶质量合格率 | |
| B. | 调查某幼儿园一班学生的平均身高 | |
| C. | 调查某市中小学生收看纪念抗日战争胜利70周年大阅兵的情况 | |
| D. | 调查某省九年级学生一周内网络自主学习的情况 |
12.(-$\frac{1}{2}$)-2等于( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
16.对于每个正整数n,抛物线y=(n2+n)x2-(2n+1)x+1与x轴交于An,Bn两点,以|AnBn|表示该两点间的距离,则|A1B1|+|A2B2|+…+|A2016B2016|的值是( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2015}{2017}$ | D. | $\frac{2016}{2017}$ |
13.已知A(1,1)、B(3,2),点B绕点A逆时针旋转90°到达点C处,则点C的坐标是( )
| A. | (0,3) | B. | (-1,3) | C. | (3,-1) | D. | (3,0) |
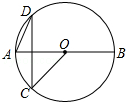 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠OCD=40°.
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠OCD=40°.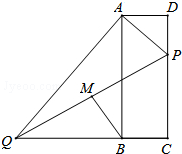 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.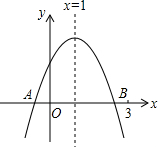 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论: