题目内容
19.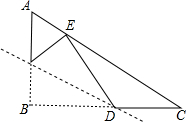 如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,点D是线段BC上一点,DC=3,沿过点D的直线折叠三角形,使点B落在斜边AC所在直线上,点B的对应点E到点A的距离是$\frac{38}{5}$-$\frac{2\sqrt{138}}{5}$.
如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,点D是线段BC上一点,DC=3,沿过点D的直线折叠三角形,使点B落在斜边AC所在直线上,点B的对应点E到点A的距离是$\frac{38}{5}$-$\frac{2\sqrt{138}}{5}$.
分析 作DF⊥AC于F,欲求AE,因为AE=AC-EF-CF,所以只要求出EF,CF,利用△CDF∽△CAB得$\frac{DF}{AB}=\frac{CF}{BC}=\frac{CD}{AC}$,可以求出CF,DF,再利用勾股定理求出EF即可.
解答 解:如图作DF⊥AC于F,
在RT△ABC中,∵AC=10,BC=8,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵∠C=∠C,∠DFC=∠ABC=90°,
∴△CDF∽△CAB,
∴$\frac{DF}{AB}=\frac{CF}{BC}=\frac{CD}{AC}$,
∴$\frac{DF}{6}=\frac{CF}{8}=\frac{3}{10}$,
∴DF=$\frac{9}{5}$,CF=$\frac{12}{5}$,
∵BD=DE=5,
在RT△DEF中,∵DE=5,DF=$\frac{9}{5}$,
∴EF=$\sqrt{{5}^{2}-(\frac{9}{5})^{2}}$=$\frac{4\sqrt{34}}{5}$,
∴AE=AC-EF-FC=10-$\frac{12}{5}$-$\frac{4\sqrt{34}}{5}$=$\frac{38}{5}$-$\frac{4\sqrt{34}}{5}$.
故答案为$\frac{38}{5}$-$\frac{4\sqrt{34}}{5}$.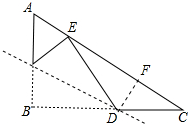
点评 本题考查翻折变换、相似三角形的判定和性质、勾股定理等知识,解题的关键是添加辅助线构造相似三角形,记住翻折不变性,属于中考常考题型.

练习册系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{x-3≤0}\\{x+2>0}\end{array}\right.$的解集是( )
| A. | x≥0 | B. | x>-2 | C. | -2<x≤3 | D. | x≤3 |
11.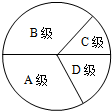 为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
根据以上提供的信息解答下列问题:
(1)若抽取的学生的数学成绩的及格率(C级及其以上为及格)为77.5%,则抽取的学生数是多少人?其中成绩为C级的学生有多少人?
(2)求出D级学生的人数在扇形统计图中的圆心角.
(3)请你估计全县数学成绩为A级的学生总人数.
 为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:| 等级 | A级(优秀) (≥108分) | B级(良好) (≥84分且<108分) | C级(及格) (≥72分且<84分) | D级(不及格) (<72分) |
| 人数 | 22 | 28 | 18 |
(1)若抽取的学生的数学成绩的及格率(C级及其以上为及格)为77.5%,则抽取的学生数是多少人?其中成绩为C级的学生有多少人?
(2)求出D级学生的人数在扇形统计图中的圆心角.
(3)请你估计全县数学成绩为A级的学生总人数.
8.与$\sqrt{5}$最接近的整数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
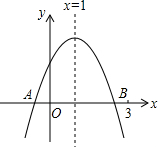 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论: