题目内容
15.观察下列各式,回答问题12+32+42=2×(12+32+3)
22+32+52=2×(22+32+6)
32+62+92=2×(32+62+18)
(1)小明用a、b、c表示等式左边由小到大的三个数,你能发现c与a、b的关系吗?
(2)你能发现等式右边括号内的是三个数与a,b之间的关系吗?请用字母a、b写出你发现的等式,并加以证明.
分析 (1)观察下列各式12+32+42=2×(12+32+3)得:1+3=4,22+32+52=2×(22+32+6)得2+3=5,32+62+92=2×(32+62+18)得3+6=9,因此发现a+b=c
(2)观察发现3=1×3,6=2×3,18=3×6,因此a2+b2+(a+b)2=2×(a2+b2+ab),证明过程只需要利用完全平方公式展开,合并同类项即可得出答案.
解答 解:(1)观察下列各式
12+32+42=2×(12+32+3)得:1+3=4
22+32+52=2×(22+32+6)得2+3=5
32+62+92=2×(32+62+18)得3+6=9
用a、b、c表示等式左边由小到大的三个数
得:a+b=c
∴c与a、b的关系为:c=a+b
(2)总结发现:a2+b2+(a+b)2=2×(a2+b2+ab)
证明如下:
a2+b2+(a+b)2
=a2+b2+a2+b2+2ab
=2a2+2b2+2ab
=2(a2+b2+ab)
点评 题目考查了规律型等式的归纳,考查学生发现问题和解决问题的能力,另外也要求学生对完全平方公式及合并同类项知识点掌握熟练,题目整体设计较好.

练习册系列答案
相关题目
5.某冷库一天的冷冻食品进出记录如表(运进用正数表示,运出用负数表示):
(1)这天冷库的冷冻食品比原来增加了还是减少了?请说明理由;
(2)根据实际情况,现有两种方案:
方案一:运进每吨冷冻食品费用500元,运出每吨冷冻食品费用800元;
方案二:不管运进还是运出每吨冷冻食品费用都是600元;
从节约运费的角度考虑,选用哪一种方案比较合适.
| 进出数量 (单位:吨) | -3 | 4 | -1 | 2 | -5 |
| 进出次数 | 2 | 1 | 3 | 3 | 2 |
(2)根据实际情况,现有两种方案:
方案一:运进每吨冷冻食品费用500元,运出每吨冷冻食品费用800元;
方案二:不管运进还是运出每吨冷冻食品费用都是600元;
从节约运费的角度考虑,选用哪一种方案比较合适.
20.对于函数y=$\frac{k}{x}$(k>0),下列说法正确的是( )
| A. | y随x的增大而减小 | B. | y随x的增大而增大 | ||
| C. | 当x<0时,y随x的增大而减小 | D. | 图象在第二、四象限内 |
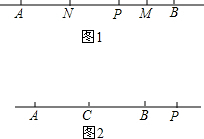 如图1,直线AB上,点P在A、B两点之间,点M为线段PB的中点,点N为线段AP的中点,若AB=m,且m为关于x的方程3x+8=2(x+m)的解.
如图1,直线AB上,点P在A、B两点之间,点M为线段PB的中点,点N为线段AP的中点,若AB=m,且m为关于x的方程3x+8=2(x+m)的解.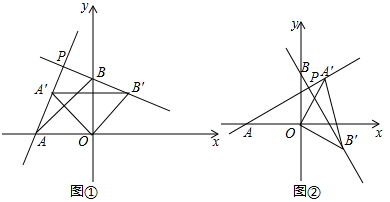
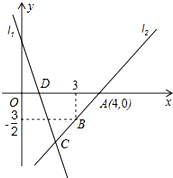 如图,已知直线l1:y=-3x+3与x轴交于点D,直线l2经过点A(4,0)、B(3,-$\frac{3}{2}$),且与l1交于点C.
如图,已知直线l1:y=-3x+3与x轴交于点D,直线l2经过点A(4,0)、B(3,-$\frac{3}{2}$),且与l1交于点C.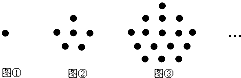 如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
如图图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )