题目内容
4.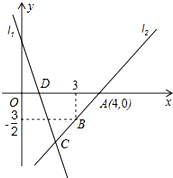 如图,已知直线l1:y=-3x+3与x轴交于点D,直线l2经过点A(4,0)、B(3,-$\frac{3}{2}$),且与l1交于点C.
如图,已知直线l1:y=-3x+3与x轴交于点D,直线l2经过点A(4,0)、B(3,-$\frac{3}{2}$),且与l1交于点C.(1)点D的坐标是(1,0).
(2)求直线l2的解析式.
(3)求△ADC的面积.
分析 (1)把y=0代入y=-3x+3解答即可;
(2)利用待定系数法解答即可;
(3)根据三角形的面积公式解答即可.
解答 解:(1)把y=0代入y=-3x+3,可得:0=-3x+3,
解得:x=1,
所以D点坐标为(1,0),
故答案为:(1,0);
(2)设直线l2的解析式为y=kx+b,
把A(4,0)、B(3,-$\frac{3}{2}$)代入得$\left\{\begin{array}{l}{4k+b=0}\\{3k+b=-\frac{3}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-6}\end{array}\right.$.
所以直线l2的解析式为y=$\frac{3}{2}$x-6;
(3)解方程组$\left\{\begin{array}{l}{y=-3x+3}\\{y=\frac{3}{2}x-6}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,
所以C点坐标为(2,-3),
所以△ADC的面积=$\frac{1}{2}$×(4-1)×3=4.5.
点评 此题考查一次函数的应用,关键是根据待定系数法求一次函数解析式.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
19.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | ${\frac{2}{3}^2}与{({\frac{2}{3}})^2}$ | D. | ${({\frac{-1}{3}})^3}与\frac{-1}{3^3}$ |
9.某店在开学初用880元购进若干个学生专用科学计算器,按每个50元出售,很快就销售一空,据了解学生还急需3倍这种计算器,于是又用2580元购进所需计算器,由于量大每个进价比上次优惠1元,该店仍按每个50元销售,最后剩下4个按九折卖出.这笔生意该店共盈利( )元.
| A. | 508 | B. | 520 | C. | 528 | D. | 560 |
13.某日温度上升了2℃记为+2,那么下降4℃记为( )
| A. | -2℃ | B. | -4℃ | C. | 2℃ | D. | 4℃ |
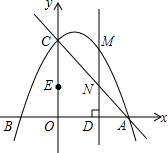 如图,抛物线y=-$\frac{1}{2}{x}^{2}+bx+c$经过A(4,0),C(0,4)两点,点B是抛物线与x轴的另一个交点,点E是OC的中点,作直线AC、点M在抛物线上,过点M作MD⊥x轴,垂足为点D,交直线AC于点N,设点M的横坐标为m,MN的长度为d.
如图,抛物线y=-$\frac{1}{2}{x}^{2}+bx+c$经过A(4,0),C(0,4)两点,点B是抛物线与x轴的另一个交点,点E是OC的中点,作直线AC、点M在抛物线上,过点M作MD⊥x轴,垂足为点D,交直线AC于点N,设点M的横坐标为m,MN的长度为d.