题目内容
6.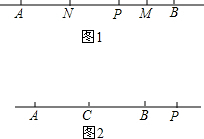 如图1,直线AB上,点P在A、B两点之间,点M为线段PB的中点,点N为线段AP的中点,若AB=m,且m为关于x的方程3x+8=2(x+m)的解.
如图1,直线AB上,点P在A、B两点之间,点M为线段PB的中点,点N为线段AP的中点,若AB=m,且m为关于x的方程3x+8=2(x+m)的解.(1)求线段AB的长;
(2)试说明线段MN的长与点P在线段AB上的位置无关;
(3)如图2,若C点为线段AB的中点,点P在线段AB的延长线上,$\frac{PA+PB}{PC}$的值是否受化?若不变,请求其值.
分析 (1)将x=m代入方程得到关于m的一元一次方程,从而可求得m的值;
(2)根据线段中点的定义可知PN=$\frac{1}{2}AP$,PM=$\frac{1}{2}PB$,从而得到MN=$\frac{1}{2}$(PA+PB)=$\frac{1}{2}AB$;
(3)先求得PB+PA的长,然后再求得PC的长,最后代入计算即可.
解答 解:(1)将x=m代入得:3m+8=4m.
解得:m=8.
故AB=8.
(2)∵M为线段PB的中点,
∴PM=$\frac{1}{2}PB$.
同理:PN=$\frac{1}{2}AP$..
∴MN=PN+PM=$\frac{1}{2}$(PB+AP)=$\frac{1}{2}×8$=4.
∴线段MN的长与点P在线段AB上的位置无关.
(3)不变.
理由:设AB=a,BP=b.则PA+PB=a+b+b=a+2b.
∵C是AB的中点,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}a$.
∴PC=PB+BC=$\frac{1}{2}a+b$.
∴$\frac{PA+PB}{PC}$=$\frac{a+2b}{\frac{1}{2}a+b}$=2.
点评 本题主要考查的是两点间的距离,掌握线段中点的定义是解题的关键.

练习册系列答案
相关题目
11.下列各式中是单项式的是( )
| A. | $\sqrt{7}$ | B. | $\sqrt{2a}$ | C. | $\frac{a-1}{2}$ | D. | $\frac{1}{a}$ |
 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,…,如此作下去,则△B2014A2015B2015的顶点A2015的坐标是(4029,$\sqrt{3}$).
在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,…,如此作下去,则△B2014A2015B2015的顶点A2015的坐标是(4029,$\sqrt{3}$).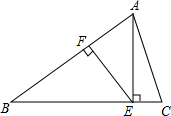 已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长.
已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长.