题目内容
9.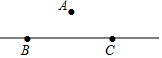 如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)
如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)
分析 连接AB,AC,过点A作BC的垂线AD,垂足为D,如图,∠1=45°,∠2=30°,AD=20m,则∠ABC=45°,∠ACB=30°,再分别计算出BD和CD得到BC的长,然后计算出汽车从点B匀速行驶到点C的速度,再通过此速度与最高限速比较大小来判断该汽车在这段限速路上是否超速.
解答 解:连接AB,AC,过点A作BC的垂线AD,垂足为D,如图,∠1=45°,∠2=30°,AD=20m,
在△ABC中,依题意∠ABC=45°,∠ACB=30°,
在△ABD中,BD=AD=20,
在Rt△ADC中,DC=$\sqrt{3}$AD=20$\sqrt{3}$=34,
∴BC=BD+DC=20+34=54,
∴汽车从点B匀速行驶到点C的速度=$\frac{54}{1.5}$=36(m/s)=129.6(km/h)>120km/h,
∴此车超速.
点评 本题考查了解直角三角形的应用-仰角俯角问题:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )
如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )
 如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )
如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )| A. | 6-π | B. | 8-π | C. | 8-2π | D. | 4 |
 已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.
已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.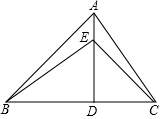 如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.
如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.