题目内容
5. 如图,点A(-3,0),B(0,2),将三角形AOB向右平移5个单位长度,再向下平移2个单位长度得到三角形CDE,点A、O、B的对应点分别为C、D、E.点P从点O开始水平向右平移,点Q从点D开始水平向左平移,速度均为每秒2个单位长度,运动时间为t秒.
如图,点A(-3,0),B(0,2),将三角形AOB向右平移5个单位长度,再向下平移2个单位长度得到三角形CDE,点A、O、B的对应点分别为C、D、E.点P从点O开始水平向右平移,点Q从点D开始水平向左平移,速度均为每秒2个单位长度,运动时间为t秒.(1)在图中画出三角形CDE,并写出C、D、E的坐标;
(2)猜想四边形BODE形状,直接写出结论,并求出四边形BODE的面积;
(3)当t为何值时,三角形BPQ的面积与三角形AOB的面积相等?
分析 (1)根据图形平移的性质画出图形,并写出C、D、E的坐标即可;
(2)根据平行四边形的判定定理即可得出结论;
(3)根据同底等高的三角形面积相等即可得出结论.
解答 解:(1)如图所示,由图可知C(2,-2),E(5,0),D(5,-2);
(2)四边形BODE是平行四边形.
∵△CDE由△AOB平移而成,
∴OB=DE,OB∥DE,
∴四边形BODE是平行四边形.
S四边形BODE=2×5=10;
(3)当Q在直线PB的右边时,
由题意:3=$\frac{1}{2}$×2×(5-2t)-$\frac{1}{2}$•2•2t-$\frac{1}{2}$•2t•2,解得t=$\frac{1}{3}$,
当Q在直线PB左边时,4×2t-$\frac{1}{2}$×4×(5-2t)=3,解得t=$\frac{4}{3}$
答:当t=$\frac{1}{3}$秒或t=$\frac{4}{3}$秒时,△BPQ的面积与△AOB的面积相等.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
14. 在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
 在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{π}{3}$ |
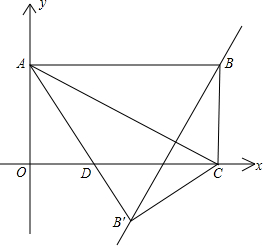 如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足:|OA-2|+OC2-4$\sqrt{3}$•OC+12=0.
如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足:|OA-2|+OC2-4$\sqrt{3}$•OC+12=0.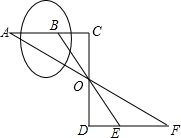 如图,某人要测量河中浅滩B和对岸A的距离,先在岸边定出点C,使C、A、B在一直线上,再在AC的垂直方向在岸边画线段CD,取它的中点O,又画DF⊥CD,观测E、O、B在一直线上,同时F、O、A也在一直线上,那么EF的长就是浅滩B和对岸A的距离,为什么?
如图,某人要测量河中浅滩B和对岸A的距离,先在岸边定出点C,使C、A、B在一直线上,再在AC的垂直方向在岸边画线段CD,取它的中点O,又画DF⊥CD,观测E、O、B在一直线上,同时F、O、A也在一直线上,那么EF的长就是浅滩B和对岸A的距离,为什么?