题目内容

19．已知平行四边形的最大角比最小角大100°，求它的各个内角的度数．

分析 由平行四边形的性质得出∠A=∠C，∠B=∠D，由四边形内角和定理得出∠A+∠B=180°，再由已知条件即可得出∠A=140°，∠B=40°，即可得出结果．

解答 解：如图所示：
∵四边形ABCD是平行四边形，
∴∠A=∠C，∠B=∠D，
∴∠A+∠C+∠B+∠D=360°，
∴∠A+∠B=180°，
又∵∠A-∠B=100°，
∴∠A=140°，∠B=40°，
∴∠A=∠C=140°，∠B=∠D=40°．

点评 本题考查了平行四边形的性质、四边形内角和定理；熟练掌握平行四边形的对角相等的性质是解决问题的关键．

练习册系列答案
相关题目
9．已知在纸面上有一数轴（如图），折叠纸面．
（1）若1表示的点与-1表示的点重合，则-7表示的点与数7表示的点重合；
（2）若-1表示的点与5表示的点重合，回答以下问题；
①12表示的点与数-8表示的点重合；
②若数轴上A、B两点之间的距离为2011（A在B的左侧），且A、B两点经折叠后重合，求A、B两点表示的数是多少？
10．说出下列各等式变形的依据进行填空．
（1）由3x-7=0得x=$\frac{7}{3}$；等式的性质1，等式的性质2．
（2）由$\frac{x}{3}-\frac{y}{2}$=0得x=$\frac{3}{2}$y；等式的性质1，等式的性质2．
（3）由$\frac{1}{2}$m-2=m得m=-4．等式的性质1，等式的性质2．
7．化简并求值：10x2+4xy-2（2y2-5x2）+4（-y2+2xy），其中x=0.5，y=-0.5．
14．已知A=3x2-5x-1，B=x2-2x-4，比较A与B的大小．
5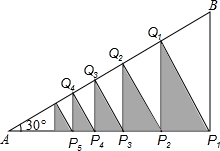．如图，在Rt△ABP1中，∠AP1B=Rt∠，∠A=30°，BP1=2，过点P1作P1Q1⊥AB，垂足Q1，过点Q1作Q1P2⊥AP1，垂足P2，过点P2作P2Q2⊥AB，垂足Q2，…如此无限下去，得到一系列阴影三角形△P1Q1P2、△P2Q2P3、△P3Q3P4…，则所有这些阴影三角形的面积和是（　　）
A．$\sqrt{3}$B．$\frac{3}{4}\sqrt{3}$C．$\frac{6}{7}\sqrt{3}$D．不能确定
12．如图，在平面直角坐标系中，点A（10，0），B（4，8），C（0，8）点P从点O出发，沿O、A、B、C路线运动，到C点停止；点Q从C点出发，沿C、B、A、O路线运动，到O停止．若点P、Q同时出发，点P的速度为1cm/s，点Q的速度为2cm/s，a秒时四边形PABC为平行四边形，此时点P、Q同时改变速度，点P的速度变为bcm/s，点Q的速度为dcm/s．图2是点P出发x秒后△OPC的面积S1（cm2）与x（s）的函数关系图象，图3是点Q出发x秒后△OQC的面积S2（cm2）与x（s）的函数关系图象．
（1）参照图2、图3，求a、b、c及d、m的值．
（2）点Q运动几秒时，OQ⊥AB，并判断此时四边形OPQB的形状．
（3）设点P离开O的路程为y1（cm），点Q距O的路程为y2（cm），请分别写出点P、Q改变速度后，y1、y2与出发后的运动时间x（s）的函数关系式．并求出P、Q相遇时x的值．
（4）当x满足2≤x≤14条件时，点P、Q在运动路线上相距的路程不大于18cm．
9．抛物线y=（x+2）（x-6）的对称轴是（　　）
A．x=-2B．x=6C．x=2D．x=4
10．假设有足够多的黑白围棋子，按照一定的规律排成一行：

请问第2015个棋子是黑的还是白的？答：白．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网