题目内容
 如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,全长68km.现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:
如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,全长68km.现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:| 2 |
| 3 |
考点:解直角三角形的应用
专题:
分析:首先过点C作CD⊥AB,垂足为D,设CD=x,即可表示出AC,BC的长,进而求出x的值,再利用锐角三角函数关系得出AD,BD的长,即可得出答案.
解答: 解:如图,过点C作CD⊥AB,垂足为D,设CD=x.
解:如图,过点C作CD⊥AB,垂足为D,设CD=x.
在Rt△ACD中,sin∠A=
,AC=
=2x,
在Rt△BCD中,sin∠B=
,BC=
=
x,
∵AC+BC=2x+
x=68
∴x=
≈
=20.
在Rt△ACD中,tan∠A=
,AD=
=20
,
在Rt△BCD中,tan∠B=
,BD=
=20,
AB=20
+20≈54,
AC+BC-AB=68-54=14.0(km).
答:隧道开通后,汽车从A地到B地比原来少走14.0千米.
 解:如图,过点C作CD⊥AB,垂足为D,设CD=x.
解:如图,过点C作CD⊥AB,垂足为D,设CD=x.在Rt△ACD中,sin∠A=
| CD |
| AC |
| CD |
| sin30° |
在Rt△BCD中,sin∠B=
| CD |
| BC |
| CD |
| sin45° |
| 2 |
∵AC+BC=2x+
| 2 |
∴x=
| 68 | ||
2+
|
| 68 |
| 2+1.4 |
在Rt△ACD中,tan∠A=
| CD |
| AD |
| CD |
| tan30° |
| 3 |
在Rt△BCD中,tan∠B=
| CD |
| BD |
| CD |
| tan45° |
AB=20
| 3 |
AC+BC-AB=68-54=14.0(km).
答:隧道开通后,汽车从A地到B地比原来少走14.0千米.
点评:此题主要考查了解直角三角形的应用,得出CD的长以及熟练选择正确的三角函数关系是解题关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
下列几组线段能组成直角三角形的是( )
| A、1,2,3 |
| B、2,4,6 |
| C、5,12,13 |
| D、7,10,11 |
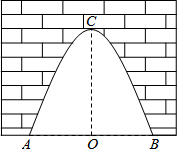 如图:某古城有一个抛物线形石拱门,拱门地面的最大宽度AB=4米,拱门的最大高度OC=4米.
如图:某古城有一个抛物线形石拱门,拱门地面的最大宽度AB=4米,拱门的最大高度OC=4米.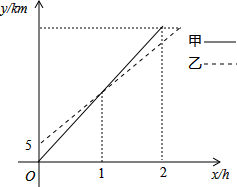 在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图.
在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图.