Question

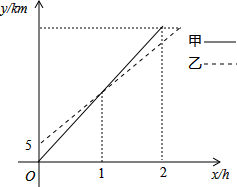在一条直线上依次有A、B、C三地，自行车爱好者甲、乙两人同时分别从A、B两地出发，沿直线匀速骑向C地．已知甲的速度为20km/h，设甲、乙两人行驶x（h）后，与A地的距离分别为y₁、y₂（km），y₁、y₂与x的函数关系如图．
（1）求y₂与x的函数关系式；
（2）若两人在出发时都配备了通话距离为3km的对讲机，求甲、乙两人在骑行过程中可以用对讲机通话的时间．

Answer 1

考点：一次函数的应用

专题：

分析：（1）根据甲的速度求出y₁=20x，然后求出x=1时的函数值，再设y₂=kx+b，然后利用待定系数法求一次函数解析式解答；
（2）分乙在前和甲在前两种情况求出距离为3km的时间，然后相减即为可以用对讲机通话的时间．

解答：解：（1）∵甲的速度为20 km/h，
∴y₁=20x，
当x=1时，y₁=20=y₂，
设y₂=kx+b，
根据题意，得，

20=k+b 5=b

，
解得

k=15 b=5

，
∴y₂=15x+5；

（2）当y₂-y₁=3时，15x+5-20x=3，x=

2

5

，
当y₁-y₂=3时，20x-（15x+5）=3，x=

8

5

，
∴

8

5

-

2

5

=

6

5

．
答：甲、乙两人在骑行过程中可以用对讲机通话的时间为

6

5

小时．

点评：本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，（1）先表示出甲的关系式是解题的关键，（2）难点在于分两种情况求出相距3km的时间．