题目内容
11.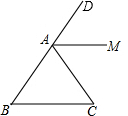 如图,在△ABC中,AB=AC,AM是外角∠DAC的平分线.
如图,在△ABC中,AB=AC,AM是外角∠DAC的平分线.(1)实践与操作:尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法),作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE.
(2)猜想并证明:∠EAC与∠DAC的数量关系并加以证明.
分析 (1)直接利用线段垂直平分线的作法得出即可;
(2)利用等腰三角形的性质结合外角的定义得出∠DAC=∠B+∠C=2∠C,进而利用线段垂直平分线的性质得出答案.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)猜想:∠EAC=$\frac{1}{2}$∠DAC,
理由如下:∵AB=AC
∴∠B=∠C,
∵∠DAC是△ABC的外角
∴∠DAC=∠B+∠C=2∠C,
∵EF垂直平分AC,
∴EA=EC,
∴∠EAC=∠C=$\frac{1}{2}$∠DAC.
点评 此题主要考查了线段垂直平分线的性质以及三角形外角的性质等知识,正确利用线段垂直平分线的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.某种病毒的直径约为0.0000000028米,该直径用科学记数法表示为( )
| A. | 0.28×10-8米 | B. | 2.8×10-10米 | C. | 2.8×10-9米 | D. | 2.8×10-8米 |
16.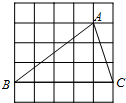 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )| A. | 1 | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{3}{4}$ |
 如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB为6m,当水位上升0.5m时:
如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB为6m,当水位上升0.5m时: