题目内容
1. 如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB为6m,当水位上升0.5m时:
如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB为6m,当水位上升0.5m时:(1)求水面的宽度CD为多少米?
(2)当水面的宽度到CD时,有一艘游船,它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行,若游船宽(指船的最大宽度)为2m,从水面到棚顶的高度为1.8m,问这艘游船能否从桥洞下通过?
分析 (1)设抛物线形桥洞的函数解析式为y=ax2+c,把A与E坐标代入求出a与c的值,确定出抛物线解析式,令y=0.5求出x的值,即可确定出CD的长;
(2)把x=1代入函数解析式求出y的值,由y-3的值与1.8比较大小即可做出判断.
解答 解:(1)设抛物线形桥洞的函数解析式为y=ax2+c,
把A(3,0),E(0,3)代入得:$\left\{\begin{array}{l}{9a+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{c=3}\end{array}\right.$,
∴y=-$\frac{1}{3}$x2+3,
由题意得:点C与D的纵坐标为0.5,
∴-$\frac{1}{3}$x2+3=0.5,
解得:x1=$\frac{\sqrt{30}}{2}$,x2=-$\frac{\sqrt{30}}{2}$,
∴CD=$\frac{\sqrt{30}}{2}$+$\frac{\sqrt{30}}{2}$=$\sqrt{30}$(米),
则水面的宽度CD为$\sqrt{30}$米;
(2)当x=1时,y=$\frac{8}{3}$,
∵$\frac{8}{3}$-0.5>1.8,
∴这艘游船能从桥洞下通过.
点评 此题考查了二次函数的应用,熟练掌握二次函数的图象与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
 如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )| A. | 点A与点C | B. | 点A与点D | C. | 点B与点C | D. | 点B与点D |
 如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么?
如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么? ,实际车牌号为100968.
,实际车牌号为100968.
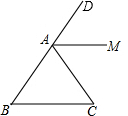 如图,在△ABC中,AB=AC,AM是外角∠DAC的平分线.
如图,在△ABC中,AB=AC,AM是外角∠DAC的平分线.