题目内容
5. 如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点.
如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点.(1)下列条件中:①AB=AC;②AD是△ABC的中线;③AD是△ABC的角平分线;④AD是△ABC的高,请选择一个△ABC满足的条件,使得四边形AEDF为菱形,并证明;
答:我选择③.(填序号)
(2)在(1)选择的条件下,△ABC再满足条件:∠BAD=90°,四边形AEDF即成为正方形.
分析 (1)根据题意和图形和容易判断题目中的哪个条件满足条件,然后针对选择的条件给出证明即可;
(2)根据有一个角是直角的菱形是正方形,即可解答本题.
解答 解:(1)我选择:③,
故答案为:③,
证明:∵DE∥AC,DF∥AB
∴四边形AEDF为平行四边形,
∵AD是△ABC的角平分线
∴∠BAD=∠DAC,
∵DE∥AC,
∴∠DAC=∠ADE,
∴∠BAD=∠ADE,
∴EA=ED,
∴平行四边形AEDF是菱形;
(2)在(1)选择的条件下,△ABC再满足条件∠BAD=90°,
故答案:∠BAD=90°,
理由:由(1)知,四边形AEDF为菱形,
∴当∠BAD=90°,四边形AEDF即成为正方形(有一个角是直角的菱形是正方形).
点评 本题考查正方形的判定、菱形的判定,解答本题的关键是明确题意,找出所求问题需要的条件,利用菱形的判定和正方形的判定解答本题.

练习册系列答案
相关题目
13.(1)填表:
(2)根据你发现的规律填空:
①已知$\root{3}{3}=1.442$,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442.
②已知$\root{3}{0.000456}$=0.07696,则$\root{3}{456}$=0.7696.
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知$\root{3}{3}=1.442$,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442.
②已知$\root{3}{0.000456}$=0.07696,则$\root{3}{456}$=0.7696.

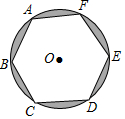 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为10;求图中阴影部分的面积.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为10;求图中阴影部分的面积.