题目内容
13.(1)填表:| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知$\root{3}{3}=1.442$,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442.
②已知$\root{3}{0.000456}$=0.07696,则$\root{3}{456}$=0.7696.
分析 (1)先通过计算填写表格;
(2)然后依据被开放数扩大或缩小1000倍,对应的立方根扩大或缩小10倍解答即可.
解答 解:(1)$\root{3}{0.0000001}$=0.01;$\root{3}{0.001}$=0.1,$\root{3}{1}$=1,$\root{3}{1000}$=10,$\root{3}{1000000}$=100,
(2)①已知$\root{3}{3}=1.442$,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442;
②已知$\root{3}{0.000456}$=0.07696,则$\root{3}{456}$=0.7696.
故答案为:14.42,0.1442,0.7696.
点评 此题考查了立方根,熟练掌握立方根的定义是解本题的关键.

练习册系列答案
相关题目
1.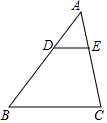 如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )
 如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
18. 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
2.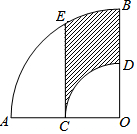 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )
 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )| A. | $\frac{4π-3\sqrt{3}}{4}$ | B. | $\frac{π-\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$+$\frac{π}{12}$ | D. | $\frac{π-3\sqrt{3}}{2}$ |
 如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=3cm,求矩形对角线的长.
如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=3cm,求矩形对角线的长. 如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点.
如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点. 如图AB=CE,AB∥CD,BC=CD,求证:△ABC≌△ECD.
如图AB=CE,AB∥CD,BC=CD,求证:△ABC≌△ECD.