题目内容
14．
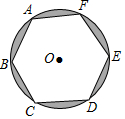如图，正六边形ABCDEF内接于⊙O，⊙O的半径为10；求图中阴影部分的面积．
分析 连接正六边形的相邻的两个顶点与圆心，构造扇形和等边三角形，则可得到弓形的面积，阴影部分的面积等于弓形的6倍．
解答 
解：连接CO、DO，
∴S阴影部分=6（S扇形OCD-S正三角形OCD）
=6（$\frac{60π×1{0}^{2}}{360}$-$\sqrt{3}$）
=100π-6$\sqrt{3}$．
点评 本题考查了正多边形与圆及扇形的面积的计算，解题的关键是知道阴影部分的面积等于三个弓形的面积．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，D为BC边上的一动点（D点不与B、C两点重合）．DE∥AC交AB于E点，DF∥AB交AC于F点．
2．
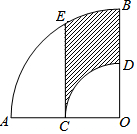如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交弧AB于点E，以点O为圆心，OC的长为半径作弧CD交OB于点D，若OA=2，则阴影部分的面积为（ ）
如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交弧AB于点E，以点O为圆心，OC的长为半径作弧CD交OB于点D，若OA=2，则阴影部分的面积为（ ）| A． | $\frac{4π-3\sqrt{3}}{4}$ | B． | $\frac{π-\sqrt{3}}{4}$ | C． | $\frac{\sqrt{3}}{2}$+$\frac{π}{12}$ | D． | $\frac{π-3\sqrt{3}}{2}$ |
画出下面几何体的从正面、从左面、从上面看到的形状图．
如图AB=CE，AB∥CD，BC=CD，求证：△ABC≌△ECD．
4．一次函数y=mx+|m|（m为常数，且m≠0）的图象过（0，2），且y随x的增大而减小，则m=（ ）
| A． | -2 | B． | 2 | C． | 1 | D． | -1 |