题目内容
19. 有一块土地形状如图所示,∠B=∠D=90°,AB=5$\sqrt{3}$m,BC=3m,CD=6$\sqrt{2}$m,请计算这块地的面积.
有一块土地形状如图所示,∠B=∠D=90°,AB=5$\sqrt{3}$m,BC=3m,CD=6$\sqrt{2}$m,请计算这块地的面积.
分析 连接AC,则△ABC和△ACD均为直角三角形,根据AB,BC可以求出AC,根据AC,CD可以求出AD,根据直角三角形面积计算可以求出△ABC和△ACD的面积,四边形ABCD的面积为两个直角三角形面积之和.
解答 解:连接AC,如图所示: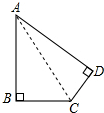
将四边形分割成两个三角形,其面积为两个三角形的面积之和,
在Rt△ABC中,AC为斜边,AB=5$\sqrt{3}$m,BC=3m,
则AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{21}$(m),
在Rt△ACD中,AC为斜边,
则AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=2$\sqrt{3}$(m),
四边形ABCD面积S=$\frac{1}{2}$AB×BC+$\frac{1}{2}$AD×CD=$\frac{1}{2}$×5$\sqrt{3}$×3+$\frac{1}{2}$×2$\sqrt{3}$×6$\sqrt{2}$=$\frac{15\sqrt{3}}{2}$+6$\sqrt{6}$(m2).
答:此块地的面积为($\frac{15\sqrt{3}}{2}$+6$\sqrt{6}$)m2.
点评 本题考查了勾股定理的应用、三角形面积的计算;熟练掌握勾股定理是解决问题的关键.

练习册系列答案
相关题目
4. 要测量池塘两端M、N的距离,小强设计了如图所示的方案,构造了△PQO≌△NMO,最后只需测出线段( )的长度.
要测量池塘两端M、N的距离,小强设计了如图所示的方案,构造了△PQO≌△NMO,最后只需测出线段( )的长度.
 要测量池塘两端M、N的距离,小强设计了如图所示的方案,构造了△PQO≌△NMO,最后只需测出线段( )的长度.
要测量池塘两端M、N的距离,小强设计了如图所示的方案,构造了△PQO≌△NMO,最后只需测出线段( )的长度.| A. | PO | B. | PQ | C. | MO | D. | MQ |
8.若多项式x2+x+m可以分解为(x+3)(x-2),则方程x2+x+m=0根是( )
| A. | x=-3 | B. | x=2 | C. | x=-3或x=2 | D. | 无法确定 |
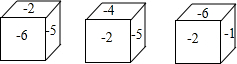 一个正方体的六个面上分别标有-1,-2,-3,-4,-5,-6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则abc=-72.
一个正方体的六个面上分别标有-1,-2,-3,-4,-5,-6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则abc=-72. 如图,一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=120°,则∠DBC的度数为60°.
如图,一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=120°,则∠DBC的度数为60°. 如图,A、B表示甲乙两个村庄,l表示河流,要在河边建一水泵站P,要求到两个村庄A、B的距离相等,用尺规作图的方法作出水泵站P的位置(要求:不写作法,保留作图痕迹)
如图,A、B表示甲乙两个村庄,l表示河流,要在河边建一水泵站P,要求到两个村庄A、B的距离相等,用尺规作图的方法作出水泵站P的位置(要求:不写作法,保留作图痕迹) 如图,已知△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长.
如图,已知△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).