题目内容
9. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).(1)建立平面直角坐标系,使点B的坐标为(-4,1),点C的坐标为(-1,1),则点A的坐标为(-3,3);
(2)画出△ABC绕原点O顺时针旋转90°后的△A1B1C1,写出A1、B1、C1的坐标,并求线段BC扫过的面积.
分析 (1)根据点C(-1,1)确定x轴和y轴,并写出点A的坐标;
(2)画出△A1B1C1,并写出A1、B1、C1的坐标,发现线段BC扫过的图形是一个不规则的图形,由图形可知:△BCO≌△B1C1O,则其面积相等,所以线段BC扫过的面积=扇形OBB1的面积-扇形ODE的面积,利用扇形面积公式代入计算即可.
解答 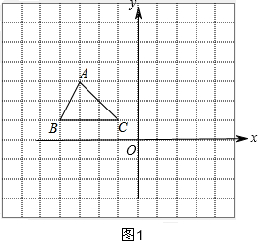 解:(1)如图1,则点A的坐标为(-3,3);
解:(1)如图1,则点A的坐标为(-3,3);
故答案为:(-3,3);
(2)如图2,A1(3,3),B1(1,4),C1(1,1),
∴线段BC扫过的面积=$\frac{90π×(\sqrt{17})^{2}}{360}$-$\frac{90π×(\sqrt{2})^{2}}{360}$=$\frac{15π}{4}$
点评 本题考查了旋转变换和扇形面积的计算问题,同时还利用点的坐标来确定其坐标轴;做好本题要熟知扇形面积的计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S=$\frac{nπ{R}^{2}}{360}$或S=$\frac{1}{2}$lR;对于求某线段扫过的面积或阴影面积问题的主要思路是:将不规则图形面积转化为规则图形的面积.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.下列结论:
①三角形至多有二条高在三角形的外部;
②一个多边形的边数每增加一条,这个多边形的内角和就增加360°;
③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;
④在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形;
其中正确的结论有( )
①三角形至多有二条高在三角形的外部;
②一个多边形的边数每增加一条,这个多边形的内角和就增加360°;
③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;
④在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形;
其中正确的结论有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )
 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )| A. | 2;SAS | B. | 4;ASA | C. | 2;AAS | D. | 4;SAS |
1.下列各组线段中,长度成比例的是( )
| A. | 1cm、2cm、3cm、4cm | B. | 3cm、5cm、9cm、15cm | ||
| C. | 2cm、4cm、6cm、8cm | D. | 1cm、3cm、5cm、7cm |
 有一块土地形状如图所示,∠B=∠D=90°,AB=5$\sqrt{3}$m,BC=3m,CD=6$\sqrt{2}$m,请计算这块地的面积.
有一块土地形状如图所示,∠B=∠D=90°,AB=5$\sqrt{3}$m,BC=3m,CD=6$\sqrt{2}$m,请计算这块地的面积.