题目内容
13．
如图，已知∠1=70°，如果CD∥BE，那么∠B的度数为（ ）| A． | 130° | B． | 70° | C． | 115° | D． | 110° |
分析 先根据补角的定义求出∠AGD的度数，再由平行线的性质即可得出结论．
解答 
解：∵∠1=70°，
∴∠AGD=180°-70°=110°．
∵CD∥BE，
∴∠B=∠AGD=110°．
故选D．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
如图，在?ABCD中，AB=8，BC=6．
1．
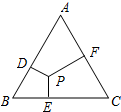如图，P为边长为2的正三角形内任意一点，过P点分别作三边的垂线，垂足分别为D，E，F，则PD+PE+PF的值为（ ）
如图，P为边长为2的正三角形内任意一点，过P点分别作三边的垂线，垂足分别为D，E，F，则PD+PE+PF的值为（ ）| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 2$\sqrt{3}$ |
18．
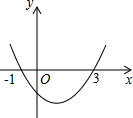已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，它与x轴的两个交点分别为（-1，0）和（3，0）．对于下列结论：①abc＞0；②b-2a=0；③a-b+c＜0；④a+b+c＞0；⑤b2-4ac＞0．其中结论正确的是（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，它与x轴的两个交点分别为（-1，0）和（3，0）．对于下列结论：①abc＞0；②b-2a=0；③a-b+c＜0；④a+b+c＞0；⑤b2-4ac＞0．其中结论正确的是（ ）| A． | ①②⑤ | B． | ①⑤ | C． | ②③ | D． | ①②③④⑤ |
3．在一个圆中，给出下列命题，其中正确的是（ ）
| A． | 若圆心到两条直线的距离都等于圆的半径，则这两条直线不可能垂直 | |
| B． | 若圆心到两条直线的距离都小于圆的半径，则这两条直线与圆一定有四个公共点 | |
| C． | 若两条弦所在直线平行，则这两条弦之间的距离一定小于圆的直径 | |
| D． | 若两条弦所在直线不平行，则这两条弦一定在圆内有公共点 |