题目内容
 如图所示,AD∥BC,DC⊥AD,AE平分∠BAD,且点E是CD的中点,问:AD、BC和AB之间有何关系?并说明理由.
如图所示,AD∥BC,DC⊥AD,AE平分∠BAD,且点E是CD的中点,问:AD、BC和AB之间有何关系?并说明理由.考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:首先要作辅助线,EF⊥AB,根据角平分线性质求出DE=EF=CE,证△BFE和△BCE全等,推出BF=BC,即可得出答案.
解答:解:AD+BC=AB,
理由是:过E作EF⊥AB于F,
∵AE平分∠DAB,DC⊥AD,
∴EF=ED,
∵E为DC中点,
∴CE=DE,
∴EF=CE,
∵AD∥BC,CD⊥AD,
∴∠C=90°=∠BFE,
在Rt△EFB和Rt△ECB中,
∴Rt△EFB≌Rt△ECB(HL),
∴BC=BF,
∵AF+BF=AB,
∴AD+BC=AB.

理由是:过E作EF⊥AB于F,
∵AE平分∠DAB,DC⊥AD,
∴EF=ED,
∵E为DC中点,
∴CE=DE,
∴EF=CE,
∵AD∥BC,CD⊥AD,
∴∠C=90°=∠BFE,
在Rt△EFB和Rt△ECB中,
|
∴Rt△EFB≌Rt△ECB(HL),
∴BC=BF,
∵AF+BF=AB,
∴AD+BC=AB.
点评:本题考查了角平分线性质,全等三角形的性质和判定的应用,此题是一道比较典型的题目,难度适中,注意:角平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目

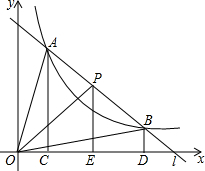 已知直线和双曲线交于A、B两点,P是线段AB上一点(P不与A、B重合),过点A、P、B分别向横坐标轴做垂线,垂足为C、D、E,连接OA、OB、OP,求证:S△POE>S△AOC=S△BOD.
已知直线和双曲线交于A、B两点,P是线段AB上一点(P不与A、B重合),过点A、P、B分别向横坐标轴做垂线,垂足为C、D、E,连接OA、OB、OP,求证:S△POE>S△AOC=S△BOD.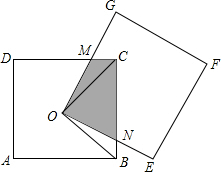 如图,正方形ABCD和正方形OEFG的边长均为4,O为正方形ABCD的中心.连接OG、OE分别与CD、BC交于M、N点,连接OC、OB.
如图,正方形ABCD和正方形OEFG的边长均为4,O为正方形ABCD的中心.连接OG、OE分别与CD、BC交于M、N点,连接OC、OB.