题目内容
2．若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{c+a}{b}$=k，则一次函数y=kx-k在平面直角坐标系内的图象必经过第一、四象限．分析 分类讨论：当a+b+c=0，利用比例性质得k=-1，则函数解析式为y=-x+1，于是一次函数与系数的关系可得直线经过第一、二、四象限；当a+b+c≠0，利用比例性质得k=$\frac{2（a+b+c）}{a+b+c}$=2，则函数解析式为y=2x-2，于是一次函数与系数的关系可得直线经过第一、三、四象限，然后综合两种情况可判断y=kx-k的图象必经过第一、四象限．
解答 解：当a+b+c=0，k=-1，则函数解析式为y=-x+1，直线y=-x+1经过第一、二、四象限；
当a+b+c≠0，$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{c+a}{b}$=k=$\frac{2（a+b+c）}{a+b+c}$=2，则函数解析式为y=2x-2，直线y=2x-2经过第一、三、四象限，
所以关于x的函数y=kx-k的图象必经过第一、四象限．
故答案为一、四．
点评 本题考查了一次函数与系数的关系：由于y=kx+b与y轴交于（0，b），当b＞0时，（0，b）在y轴的正半轴上，直线与y轴交于正半轴；当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．记住k＞0，b＞0?y=kx+b的图象在一、二、三象限；k＞0，b＜0?y=kx+b的图象在一、三、四象限；k＜0，b＞0?y=kx+b的图象在一、二、四象限；k＜0，b＜0?y=kx+b的图象在二、三、四象限．也考查了比例的性质．
练习册系列答案
相关题目
12．梯形上底为a，下底为b，高为（2a-b），则梯形的面积是（ ）
| A． | ${a^2}+\frac{1}{2}ab-\frac{1}{2}{b^2}$ | B． | 2a2+ab-b2 | C． | ${a^2}-\frac{1}{2}{b^2}$ | D． | ${a^2}+ab-\frac{1}{2}{b^2}$ |
13．若0是一元二次方程（m-1）x2+6x+m2-1=0的一个根，则m取值为（ ）
| A． | 1 | B． | -1 | C． | ±1 | D． | 以上都不是 |
14．八边形的对角线共有（ ）
| A． | 8条 | B． | 16条 | C． | 18条 | D． | 20条 |
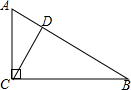如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．
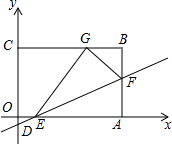如图，矩形OABC的边OA在x轴上，边OC在y轴上，点B在第一象限，直线y=$\frac{1}{3}$x-1与x轴、y轴、边AB分别交于点E，点D，点F，将△AEF沿直线EF折叠，点A恰好落在BC边的点G位置上，线段AF，BF的长是一元二次方程x2-9x+20=0的两根（AF＞BF）．