题目内容
12.正方体ABCD的边长为1,点E在边AB上,BE=$\frac{1}{4}$,BF=$\frac{1}{7}$,动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,而当碰到正方形顶点时沿入射路径反弹,当点P第一次返回E时,P所经过的路程为( )| A. | $\sqrt{65}$ | B. | $\frac{3\sqrt{65}}{2}$ | C. | 2$\sqrt{65}$ | D. | $\frac{5\sqrt{65}}{2}$ |
分析 根据已知中的点E,F的位置,可知入射角的正切值为$\frac{7}{4}$,通过相似三角形,来确定反射后的点的位置,从而可得反射的次数.再由勾股定理就可以求出小球经过的路径的总长度.
解答 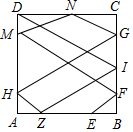 解:根据已知中的点E,F的位置,可知入射角的正切值为$\frac{7}{4}$,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得第二次碰撞点为M,在DA上,且DM=$\frac{2}{7}$DA,第三次碰撞点为N,在DC上,且DN=$\frac{1}{2}$DC,第四次碰撞点为G,在CB上,且CG=$\frac{2}{7}$BC,第五次碰撞点为H,在DA上,且AH=$\frac{1}{7}$AD,第六次碰撞点为Z,在AB上,且AZ=$\frac{1}{4}$AD,第七次碰撞点为I,在BC上,且BI=$\frac{3}{7}$AD,第八次碰撞点为D,再反方向可到E,
解:根据已知中的点E,F的位置,可知入射角的正切值为$\frac{7}{4}$,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得第二次碰撞点为M,在DA上,且DM=$\frac{2}{7}$DA,第三次碰撞点为N,在DC上,且DN=$\frac{1}{2}$DC,第四次碰撞点为G,在CB上,且CG=$\frac{2}{7}$BC,第五次碰撞点为H,在DA上,且AH=$\frac{1}{7}$AD,第六次碰撞点为Z,在AB上,且AZ=$\frac{1}{4}$AD,第七次碰撞点为I,在BC上,且BI=$\frac{3}{7}$AD,第八次碰撞点为D,再反方向可到E,
由勾股定理可以得出EF=HZ=$\sqrt{(\frac{1}{4})^{2}+(\frac{1}{7})^{2}}$=$\frac{\sqrt{65}}{28}$,FM=GH=ID=$\frac{4\sqrt{65}}{28}$,MN=NG=$\frac{2\sqrt{65}}{28}$,ZI=$\frac{3\sqrt{65}}{28}$,
P所经过的路程为($\frac{\sqrt{65}}{28}$×2+$\frac{4\sqrt{65}}{28}$×3+$\frac{2\sqrt{65}}{28}$×2+$\frac{3\sqrt{65}}{28}$)×2=$\frac{3\sqrt{65}}{2}$.
故选:B.
点评 本题主要考查了反射原理与三角形相似知识的运用.通过相似三角形的性质来确定反射后的点的位置,从而可得反射的次数,由勾股定理来确定小球经过的路程,是一道数学物理学科综合试题,难度较大.

 名校课堂系列答案
名校课堂系列答案| A. | 2ab+3ab=5a2b2 | B. | a2•a3=a6 | C. | a-2=$\frac{1}{{a}^{2}}$(a≠0) | D. | $\sqrt{x+y}=\sqrt{x}+\sqrt{y}$ |
| A. | 1.28m | B. | 1.13m | C. | 0.64m | D. | 0.32m |


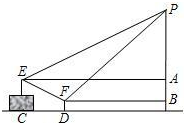 广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)
广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)