题目内容
17.世界杯足球赛小组赛规定,每个小组4个队进行单循环比赛,每场比赛胜队得3分,败队得0分,平局时两队各得1分,小组赛完后,总积分最高的2个队出线进入下轮比赛,如果总积分相同,还要按净胜球数排序,一个队要保证出线,这个队至少要积( )分.| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
分析 首先根据题意推出6场比赛后各队的得分之和不超过18分,再分两种情形讨论①若一个队得7分,②若一个队得6分,看看其他队的得分的可能性,即可解决问题.
解答 解:4个队进行单循环比赛共比赛4×3÷2=6场,每场比赛后两队得分之和或为2分或为2分,所以6场比赛后各队的得分之和不超过18分,
①若一个队得7分,剩下的3个队得分之和不超过11分,不可能有两个队得分都大于或等于7分,所以这个队必定出线.
②若一个队得6分,则有可能还有两个队均得6分,而净胜球比该队多,该队仍不能出线.
故选B.
点评 本题考查了比赛问题中的推理与论证;得到比赛的总场数以及相应的总积分是解决本题的突破点;分类探讨可以出线的小组的最低分是解决本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.不等式组$\left\{\begin{array}{l}{-3(x+1)-x<5}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1}\end{array}\right.$的解为( )
| A. | x<-2或x≥1 | B. | x<-2 | C. | -2<x≤1 | D. | -2$<x<\frac{1}{2}$ |
12.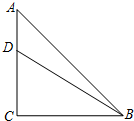 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
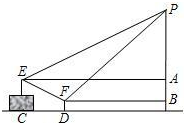 广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)
广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号) 已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG.
已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG.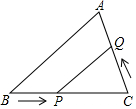 如图,在△ABC中,∠C=90°,BC=8cm,4AC-3BC=0,点P从B点出发,沿BC方向以2cm/s的速度移动,点Q从C点出发,沿CA方向以1cm/s的速度移动,若P、Q分别从B、C同时出发,经过多少秒时,△CPQ与△CBA相似?
如图,在△ABC中,∠C=90°,BC=8cm,4AC-3BC=0,点P从B点出发,沿BC方向以2cm/s的速度移动,点Q从C点出发,沿CA方向以1cm/s的速度移动,若P、Q分别从B、C同时出发,经过多少秒时,△CPQ与△CBA相似?