题目内容
17. 如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
分析 利用“有一组邻边相等的平行四边形是菱形”证明四边形CDEF是菱形.即先证明CD=DE,再证明四边形CDEF为平行四边形.
解答 解:四边形CDEF是菱形.理由如下:
∵△ABC中,∠ACB=90°,
∴DC⊥CB,
又∵DE⊥AB于E,且∠ABC的平分线BD交AC于点D,
∴CD=DE(角平分线上的点到角的两边的距离相等)
在△CBD与△EBD中,$\left\{\begin{array}{l}{∠BCD=∠BED=90°}\\{∠CBD=∠EBD(角平分线的性质)}\\{BD=BD(公共边相等)}\end{array}\right.$
∴△CBD≌△EBD
∴∠CDF=∠EDF
又在△CDF与△EDF中,$\left\{\begin{array}{l}{CD=DE}\\{∠CDF=∠EDF}\\{FD=FD}\end{array}\right.$
∴△CDF≌△EDF
∴∠FCD=∠FED
又CH⊥AB于H,且交BD于点F,DE⊥AB于E,
∴CF∥DE,∠HFE=∠FED,
∴∠HFE=∠FCD
∴EF∥CD
∴四边形CDEF是平行四边形,
又CD=DE
∴四边形CDEF是菱形(有一组邻边相等的平行四边形是菱形)
点评 本题考查了角平分线的性质、菱形的判定等知识点,解题的关键是要掌握菱形的判定方法与角平分线的性质等知识要点的综合应用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
9.已知x≠y,下列各式与$\frac{x-y}{x+y}$相等的是( )
| A. | $\frac{(x-y)+5}{(x+y)+5}$ | B. | $\frac{2x-y}{2x+y}$ | C. | $\frac{(x-y)^{2}}{{x}^{2}-{y}^{2}}$ | D. | $\frac{{x}^{2}-{y}^{2}}{{x}^{2}+{y}^{2}}$ |
 如图,点P1在四边形ABCD的内部,点P2在边CD上,直线l在四边形ABCD外.
如图,点P1在四边形ABCD的内部,点P2在边CD上,直线l在四边形ABCD外. 某校八年级全体320名学生在电脑培训前、后分别参加了一次水平相同的考试,考分都以同一标准划分成“不合格”“合格”“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示,试结合图示信息回答下列问题:
某校八年级全体320名学生在电脑培训前、后分别参加了一次水平相同的考试,考分都以同一标准划分成“不合格”“合格”“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示,试结合图示信息回答下列问题: 如图,已知⊙O的弦AB=3,点C在⊙O上,且∠ACB=60°,则⊙O的直径是2$\sqrt{3}$.
如图,已知⊙O的弦AB=3,点C在⊙O上,且∠ACB=60°,则⊙O的直径是2$\sqrt{3}$.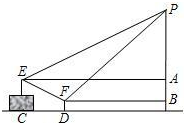 广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)
广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)