题目内容
 已知动点A在反比例函数y=
已知动点A在反比例函数y=| k |
| x |
| A、1 | B、2 | C、4 | D、12 |
考点:反比例函数系数k的几何意义
专题:
分析:根据图象上的点在函数图象上,可得A点坐标,根据AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AC,可得D、E点坐标,根据待定系数法,可得DE的解析式,根据三角形的面积公式,可得关于k的一元一次方程,根据解方程,可得答案.
解答:解:如图:
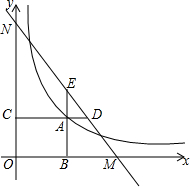 ,
,
由动点A在反比例函数y=
(k>0)的图象上,设A(m,
).
由AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AC,延长BA至点E,使AE=AB,得
D(2m,
),E(m,
).
设直线DE的解析式是y=Kx+b,图象过点D、E,得
,解得
.
直线DE的解析式是y=-
x+
.
当x=0时,y=
即N(0,
),
当y=0时,x=3m,即M(3m,0).
S△MON=
OM•ON=
×
×3m=18.
解得k=4,
故选;C.
 ,
,由动点A在反比例函数y=
| k |
| x |
| k |
| m |
由AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AC,延长BA至点E,使AE=AB,得
D(2m,
| k |
| m |
| 2k |
| m |
设直线DE的解析式是y=Kx+b,图象过点D、E,得
|
|
直线DE的解析式是y=-
| k |
| m2 |
| 3k |
| m |
当x=0时,y=
| 3k |
| m |
| 3k |
| m |
当y=0时,x=3m,即M(3m,0).
S△MON=
| 1 |
| 2 |
| 1 |
| 2 |
| 3k |
| m |
解得k=4,
故选;C.
点评:本题考查了反比例函数系数k的几何意义,利用了图象上的点满足函数解析式,解二元一次方程组,三角形的面积公式,解一元一次方程.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
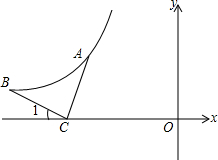 如图,反比例函数y=
如图,反比例函数y= 已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若
已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若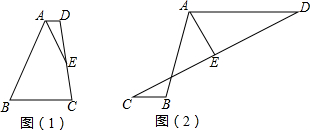
 如图,点A、B、C、D为⊙O上的点,∠ABC=90°,若AD=8,tan∠DBC=
如图,点A、B、C、D为⊙O上的点,∠ABC=90°,若AD=8,tan∠DBC=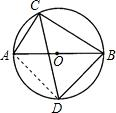 如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是
如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是