题目内容
⊙O的周长为a cm，面积为a cm2，如果点O到一条直线的距离为π cm，则这条直线与⊙O有怎样的位置关系？
考点：直线与圆的位置关系
专题：
分析：首先利用圆的周长公式以及面积公式进而求出圆的半径，进而利用半径与点O到一条直线的距离为π cm，的关系得出直线与⊙O的位置关系．
解答：解：∵圆O的周长为a cm，则2πr=a①
面积为a cm2，则πr2=a②
②÷①得：
=1，
解得：r=2
∵点O到一条直线的距离为πcm＞半径2cm，
所以直线与圆是相离．
面积为a cm2，则πr2=a②
②÷①得：
| r |
| 2 |
解得：r=2
∵点O到一条直线的距离为πcm＞半径2cm，
所以直线与圆是相离．
点评：此题主要考查了直线与圆的位置关系，求出圆的半径是解题关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
下列说法正确的是（ ）
| A、若|a|=|b|，则a=b |
| B、如果a2=3a，那么a=3 |
| C、若|a|+b2=0时，则a+b=0 |
| D、若|a|=-a，则a≤0 |
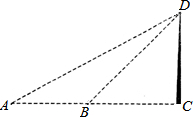如图所示，在上海黄浦江西岸一点B处，测得东方明珠电视塔尖D的仰角为45°，后退20m到A处，测得塔尖D的仰角为30°，A、B、C在同一直线上，求电视塔的高度．
已知动点A在反比例函数y=
如图，AB是⊙O的直径，点C在AB的延长线上，AB=2BC，点D在⊙O上，∠DAO=30°．
如图，AD是△ABC的外接圆直径，AD=6cm，∠B=∠DAC，则AC的值为