题目内容
 如图,点O是AC上一点,OE,OF分别平分∠AOB,∠BOC.
如图,点O是AC上一点,OE,OF分别平分∠AOB,∠BOC.(1)求∠EOF的大小.
(2)当OB绕O点旋转时,若OE,OF仍为∠AOB和∠BOC的平分线,问:OE,OF有怎样的位置关系?
考点:角平分线的定义
专题:
分析:(1)先由点O是AC上一点,得出∠AOB+∠BOC=∠AOC=180°,再由OE,OF分别平分∠AOB,∠BOC,根据角平分线定义得出∠BOE=
∠AOB,∠BOF=
∠BOC,那么∠EOF=∠BOE+∠BOF=
∠AOB+
∠BOC=
∠AOC=90°;
(2)当OB绕O点旋转时,若OE,OF仍为∠AOB和∠BOC的平分线,仍然可以得到∠EOF=90°,根据垂直的定义得出OE⊥OF.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)当OB绕O点旋转时,若OE,OF仍为∠AOB和∠BOC的平分线,仍然可以得到∠EOF=90°,根据垂直的定义得出OE⊥OF.
解答:解:(1)∵点O是AC上一点,
∴∠AOB+∠BOC=∠AOC=180°,
∵OE,OF分别平分∠AOB,∠BOC,
∴∠BOE=
∠AOB,∠BOF=
∠BOC,
∴∠EOF=∠BOE+∠BOF
=
∠AOB+
∠BOC
=
∠AOC
=90°;
(2)当OB绕O点旋转时,若OE,OF仍为∠AOB和∠BOC的平分线,仍然可以得到∠EOF=90°,所以OE⊥OF.
∴∠AOB+∠BOC=∠AOC=180°,
∵OE,OF分别平分∠AOB,∠BOC,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠BOE+∠BOF
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=90°;
(2)当OB绕O点旋转时,若OE,OF仍为∠AOB和∠BOC的平分线,仍然可以得到∠EOF=90°,所以OE⊥OF.
点评:本题考查了角平分线定义,平角的定义,垂直的定义,是基础题,比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据等式的性质,下列变形正确的是( )
A、若x=y,则
| ||||
| B、若x=y,则x-2=2-y | ||||
| C、如果2x=y,那么-6x=-3y | ||||
D、如果
|
关于x的方程
+3=
有增根,则m的值为( )
| 7 |
| x-1 |
| m |
| x-1 |
| A、x=1 | B、x=-1 |
| C、x=7 | D、x=-7 |

 如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O的切线FE交AC于点E.
如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O的切线FE交AC于点E.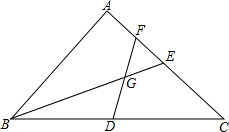 已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.