题目内容
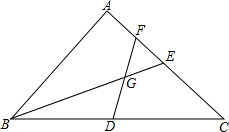 已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.(1)若E为AC上任意一点,连接AG,求证:∠EAG=∠ABE.
(2)若E为AC中点,则EF:FD=
考点:相似三角形的判定与性质
专题:
分析:(1)如图,连接AD,证明A、B、D、G四点共圆,即可解决问题.
(2)如图,连接DE;证明AF=2EF=2λ;证明DE=3λ;证明∠DEF=90°,求出DF=
λ,即可解决问题.
(2)如图,连接DE;证明AF=2EF=2λ;证明DE=3λ;证明∠DEF=90°,求出DF=
| 10 |
解答: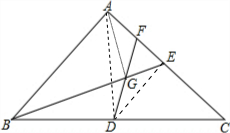 解:(1)如图,连接AD;
解:(1)如图,连接AD;
∵∠A=90°,AB=AC,D为BC中点,
∴∠ADB=90°,DA=DB;
∴∠DAB=∠ABD=45°;
∵∠BGD=∠EGF=45°,
∴A、B、D、G四点共圆,
∴∠AGB=∠ADB=90°,
即AG⊥BE;
∴∠ABE+∠BAG=∠BAG+∠EAG,
∴∠EAG=∠ABE.
(2)如图,连接DE;
∵∠AGE=90°,∠EGF=45°,
∴∠AGF=∠EGF=45°,
∴AF:EF=AG:EG;
∵∠BAE=∠AGE=90°,∠EAG=∠ABE,
∴△ABE∽△GAE,
∴AB:AE=AG:GE=2:1,
∴AF=2EF(设EF为λ);
∵点E为AC的中点,
∴AB=AC=6λ;
∵点D、E分别为BC、AC的中点,
∴DE∥AB,DE=
AB=3λ,
∴∠DEF=90°;
由勾股定理得:DF2=EF2+DE2=10λ2,
∴DF=
λ,
EF:DF=λ:
λ=1:
,
故答案为1:
.
 解:(1)如图,连接AD;
解:(1)如图,连接AD;∵∠A=90°,AB=AC,D为BC中点,
∴∠ADB=90°,DA=DB;
∴∠DAB=∠ABD=45°;
∵∠BGD=∠EGF=45°,
∴A、B、D、G四点共圆,
∴∠AGB=∠ADB=90°,
即AG⊥BE;
∴∠ABE+∠BAG=∠BAG+∠EAG,
∴∠EAG=∠ABE.
(2)如图,连接DE;
∵∠AGE=90°,∠EGF=45°,
∴∠AGF=∠EGF=45°,
∴AF:EF=AG:EG;
∵∠BAE=∠AGE=90°,∠EAG=∠ABE,
∴△ABE∽△GAE,
∴AB:AE=AG:GE=2:1,
∴AF=2EF(设EF为λ);
∵点E为AC的中点,
∴AB=AC=6λ;
∵点D、E分别为BC、AC的中点,
∴DE∥AB,DE=
| 1 |
| 2 |
∴∠DEF=90°;
由勾股定理得:DF2=EF2+DE2=10λ2,
∴DF=
| 10 |
EF:DF=λ:
| 10 |
| 10 |
故答案为1:
| 10 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
 如图,点O是AC上一点,OE,OF分别平分∠AOB,∠BOC.
如图,点O是AC上一点,OE,OF分别平分∠AOB,∠BOC. 在△ABC中,AB=AC,BD平分∠ABC交AC于点D,若BD=BC,且AB=20,求BC的长.
在△ABC中,AB=AC,BD平分∠ABC交AC于点D,若BD=BC,且AB=20,求BC的长.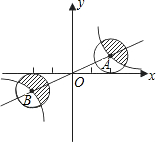 如图,正比例函数与反比例函数的图象相交于AB、两点,分别以AB、两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )
如图,正比例函数与反比例函数的图象相交于AB、两点,分别以AB、两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )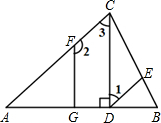 已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.
已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.