题目内容
9.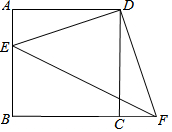 如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.
如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.(1)求证:△ADE≌△CDF;
(2)连接EF,若AB=3,AE=1,求EF的长.
分析 (1)根据两边及其夹角分别对应相等的两个三角形全等进行证明即可;
(2)先求得BE=3-1=2,BF=3+1=4,再根据勾股定理,在Rt△BEF中,求得EF即可.
解答  解:(1)∵正方形ABCD中,∠A=∠BCD=90°,则
解:(1)∵正方形ABCD中,∠A=∠BCD=90°,则
∠DCF=∠A=90°,AD=CD,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{AD=CD}\\{∠A=∠DCF}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CDF(SAS);
(2)∵AB=BC=3,CF=AE=1,
∴BE=3-1=2,BF=3+1=4,
∴Rt△BEF中,EF=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$.
点评 本题主要考查了正方形的性质,全等三角形的判定以及勾股定理的运用,解题时注意:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
2.下列关于等边三角形的描述错误的是( )
| A. | 三边相等的三角形是等边三角形 | |
| B. | 三个角相等的三角形是等边三角形 | |
| C. | 有一个角是60°的三角形是等边三角形 | |
| D. | 有两个角是60°的三角形是等边三角形 |
18.若2amb3与-3a4bn是同类项,则m,n的值分别为( )
| A. | 2,1 | B. | 3,4 | C. | 3,2 | D. | 4,3 |
 如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(-1,m)两点,与x轴交于点C.
如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(-1,m)两点,与x轴交于点C.
 作图题(要求尺规作图,不写作法,保留作图痕迹)
作图题(要求尺规作图,不写作法,保留作图痕迹)