题目内容
17. 如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(-1,m)两点,与x轴交于点C.
如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(-1,m)两点,与x轴交于点C.(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA、OB,求△AOB的面积.
分析 (1)利用待定系数法求出反比例函数和一次函数的解析式;
(2)根据一次函数的解析式求出OC,根据三角形的面积公式计算即可.
解答 解:(1)设反比例函数的解析式为y=$\frac{k}{x}$,一次函数的解析式为y=ax+b,
点A(2,1)在反比例函数的图象上,
∴k=2,
则反比例函数的解析式为y=$\frac{2}{x}$,
当x=-1时,m=$\frac{2}{-1}$=-2,
∴当B(-1,-2),
$\left\{\begin{array}{l}{2a+b=1}\\{-a+b=-2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,
∴反比例函数的解析式为y=$\frac{2}{x}$,一次函数的解析式为y=x-1;
(2)∵直线AB的解析式为y=x-1,
∴OC=1,
∴△AOB的面积=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=$\frac{3}{2}$.
点评 本题考查的是反比例函数与一次函数的交点问题,掌握待定系数法求函数解析式是一般步骤是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若2m=3,2n=4,则23m+2n等于( )
| A. | 432 | B. | $\frac{9}{16}$ | C. | 11 | D. | 1 |
5.下列计算正确的是( )
| A. | $\sqrt{3}$×$\sqrt{2}$=6 | B. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
 如图是由五个正方体搭成的立体模型,从上面看到的形状图是( )
如图是由五个正方体搭成的立体模型,从上面看到的形状图是( )



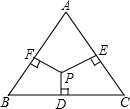 如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,求点P到三角形的三边的距离之和PD+PE+PF的值.
如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,求点P到三角形的三边的距离之和PD+PE+PF的值.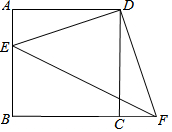 如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.
如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.