题目内容
4.已知将一副三角板(直角三角板OAB和直角三角板OCD,∠AOB=90°,∠COD=30°)如图1摆放,点O、A、C在一条直线上,将直角三角板OCD绕点O逆时针方向转动,变化摆放如图位置(1)如图2,当∠OAC为多少度时,OB恰好平分∠COD?
(2)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC,射线ON平分∠BDO,如果三角形OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由
(3)如图4,当三角板OCD转到∠AOB外部时,射线OM、ON仍然分别平分∠AOC、∠BOD,在旋转过程中,(2)中的结论是否成立?如果结论成立,请说明理由;如果不成立,请写出你的结论并根据图4说明理由.
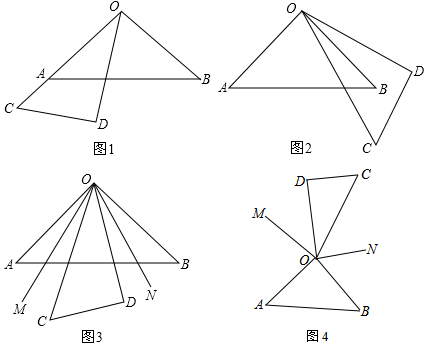
分析 (1)由图可得角之间的关系:∠BOD=90°-∠COD,∠AOC=90°-$\frac{1}{2}$∠COD,据此解答;
(2))由图可得角之间的关系:∠MON=$\frac{1}{2}$(∠AOB-∠COD)+∠COD,于是得到结论;
(3)由图可得角之间的关系;∠MON=∠MOC+∠NOD-30°,于是得到结论.
解答 解:∵∠BAC+∠ABP+∠BPF+∠AFP=360°,且∠BPF+∠BAC=180°,
∴∠ABP+∠AFP=180°,
(1)∵OB平分∠COD,∠COD=30°,
∴∠BOC=$\frac{1}{2}$∠COD=15°,
∴∠AOC=∠AOB-∠BOC=90°-15°=75°,
(2)∵∠AOB=90°,∠COD=30°,
∴∠AOC+∠BOD=90°-30°=60°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC+∠NOD=$\frac{1}{2}$∠AOC+∠BOD)=30°,
∴∠MON=∠COD+∠MOC+∠NOD=30°+30°=60°,
(3)∵∠AOB=90°,∠COD=30°,
∴∠AOC+∠BOD=360°-90°+∠COD=300°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC+∠NOD=$\frac{1}{2}$(∠AOC+∠BOD)=150°,
∴∠MON=∠MOC+∠NOD-∠COD=150°-30°=120°.
点评 本题考查了角的计算,难点是找出变化过程中的不变量,需要结合图形来计算,对同学们的作图、分析、计算能力有较高要求.在计算分析的过程中注意动手操作,在旋转的过程中得到不变的量.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
15. 如图所示,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角△ABC,∠BAC=90°,试求经过B、C两点的直线的函数表达式.
如图所示,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角△ABC,∠BAC=90°,试求经过B、C两点的直线的函数表达式.
 如图所示,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角△ABC,∠BAC=90°,试求经过B、C两点的直线的函数表达式.
如图所示,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角△ABC,∠BAC=90°,试求经过B、C两点的直线的函数表达式.
19.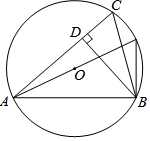 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
13.如图是从不同方向看某个几何体得到的图形,则这个几何体是( )


| A. | 正方体 | B. | 长方体 | C. | 圆柱 | D. | 球 |
 如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.
如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF. 小明和小强分别从A、B两地出发匀速相向而行,达到对方出发地后均立即以原速返回.已知小明到达B地半小时后,小强到达A地.如图表示他们出发时间t(单位:小时)与距离A地的路程S(单位:千米)之间的关系图,则出发后$\frac{45}{11}$小时,小明和小强第2次相遇.
小明和小强分别从A、B两地出发匀速相向而行,达到对方出发地后均立即以原速返回.已知小明到达B地半小时后,小强到达A地.如图表示他们出发时间t(单位:小时)与距离A地的路程S(单位:千米)之间的关系图,则出发后$\frac{45}{11}$小时,小明和小强第2次相遇.