题目内容
14.A,B两队正在进行一系列比赛,若两队中任何一队赢得一盘的机会都是均等的,但为了在一系列比赛中获胜,A队必须赢2盘,B队必须赢3盘,那么A队获胜的概率是$\frac{11}{16}$.分析 B队获胜的条件是,B队在A队赢2盘之前赢3盘,即B队赢了的时候,A队或者一盘都没赢,或者只赢了一盘.计算出B队获胜概率,用1减去B队获胜概率可得.
解答 解:根据题意,B队获胜的条件是,B队在A队赢2盘之前赢3盘,即B队赢了的时候,A队或者一盘都没赢,或者只赢了一盘.
B队获胜的情况有下面四种:(1)BBB;(2)ABBB;(3)BABB;(4)BBAB
∴B队获胜的概率为:$(\frac{1}{2})^{3}+(\frac{1}{2})^{4}+(\frac{1}{2})^{4}+(\frac{1}{2})^{4}$=$\frac{5}{16}$,
那么,A队获胜的概率为1-$\frac{5}{16}$=$\frac{11}{16}$,
故答案为:$\frac{11}{16}$.
点评 本题主要考查列举法求概率能力,根据题意列出所有可能结果是求概率的根本,本题从反面求概率的思路是关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
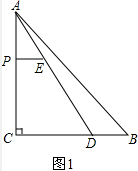 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围.