题目内容
2.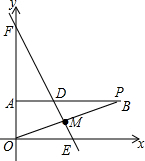 如图,在平面直角坐标系中,点A的坐标为(0,2),AB⊥y轴,点P是第一象限内射线AB上的一点,线段OP的垂直平分线分别交射线AB,x轴,y轴于点D,E,P,当PA=OA+OE时,则点D的坐标为(2,2).
如图,在平面直角坐标系中,点A的坐标为(0,2),AB⊥y轴,点P是第一象限内射线AB上的一点,线段OP的垂直平分线分别交射线AB,x轴,y轴于点D,E,P,当PA=OA+OE时,则点D的坐标为(2,2).
分析 根据AB⊥y轴,OE⊥x轴,得到AB∥OE,根据平行线的性质得到∠OPA=∠EOP,推出△OEM≌△PDM,根据全等三角形的性质得到OE=PD,根据已知条件即可得到结论.
解答 解:∵AB⊥y轴,OE⊥x轴,
∴AB∥OE,
∴∠OPA=∠EOP,
在△OEM与△PDM中,$\left\{\begin{array}{l}{∠OPA=∠EOP}\\{∠OME=∠PMA}\\{OM=MP}\end{array}\right.$,
∴△OEM≌△PDM,
∴OE=PD,
∵PA=OA+OE,PA=AD+PD,
∴OA=AD=2,
∴D(2,2).
故答案为:(2,2).
点评 本题考查了全等三角形的判定和性质,平行线的性质,坐标与图形的性质,线段垂直平分线的性质,证得△OEM≌△PDM是解题的关键.

练习册系列答案
相关题目
6. 已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|+|b+2|的结果是( )
已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|+|b+2|的结果是( )
 已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|+|b+2|的结果是( )
已知a,b两数在数轴上的位置如图所示,则化简代数式|a+b|-|a-1|+|b+2|的结果是( )| A. | 1 | B. | 2a-3 | C. | 2b+3 | D. | -1 |
11.下列说法正确的是( )
| A. | 90°的角叫余角,180°的角叫补角 | |
| B. | 如果∠1+∠2+∠3=180°,那么∠1、∠2与∠3互补 | |
| C. | 如果两个角相等,那么它们的补角相等 | |
| D. | 如果∠α>∠β,那么∠α的补角比∠β的补角大 |
11.用配方法解方程x2-4x+3=0的过程中,配方正确的是( )
| A. | (x-2)2=1 | B. | (x+2)2=4 | C. | (x-2)2=-1 | D. | (x-2)2=3 |
12.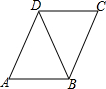 如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
 如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )| A. | △ABD和△CDB的面积相等 | B. | △ABD和△CDB的周长相等 | ||
| C. | AD∥BC,且AD=BC | D. | ∠A+∠ABD=∠C+∠CBD |
 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为6.
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为6. 如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对的两个面上的代数式的值相等,求2a+b-3c的值.
如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对的两个面上的代数式的值相等,求2a+b-3c的值. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.