题目内容
7. 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为6.
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为6.
分析 先根据垂径定理求出AD的长,再由AAS定理得出△ADO≌△OFE,推出OF=AD即可求出答案.
解答 解:∵OD⊥AC,AC=12,
∴AD=CD=6,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵OE∥AC,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EF=90°,
∴∠DAO=∠EOF,
在△ADO和△OFE中,$\left\{\begin{array}{l}{∠ADO=∠EFO}&{\;}\\{∠DAO=∠FOE}&{\;}\\{OA=OE}&{\;}\end{array}\right.$,
∴△ADO≌△OFE(AAS),
∴OF=AD=6,
故答案为:6.
点评 本题考查了垂径定理、全等三角形的性质和判定等知识;熟练掌握垂径定理,证明△ADO≌△OFE是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.书架上有数学书2本,英语书3本,语文书5本,从中任意抽取一本是数学书的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{5}$ |
2.记者从歌华有线大样本数据研究中心了解到:本市启动空气重污染红色预警后,通过电视课堂学习的中小学生迅速增加,12月8日0时至24时,歌华有线高清交互数字电视平台“北京数字学校”栏目总访问量超过1 010 000次,中小学生通过电视课堂实现了“停课不停学”.将1 010 000用科学记数法表示为( )
| A. | 101×104 | B. | 10.1×105 | C. | 1.01×106 | D. | 0.101×107 |
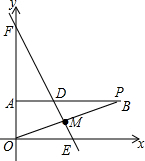 如图,在平面直角坐标系中,点A的坐标为(0,2),AB⊥y轴,点P是第一象限内射线AB上的一点,线段OP的垂直平分线分别交射线AB,x轴,y轴于点D,E,P,当PA=OA+OE时,则点D的坐标为(2,2).
如图,在平面直角坐标系中,点A的坐标为(0,2),AB⊥y轴,点P是第一象限内射线AB上的一点,线段OP的垂直平分线分别交射线AB,x轴,y轴于点D,E,P,当PA=OA+OE时,则点D的坐标为(2,2).