题目内容
19.已知:实数x满足$\frac{3x-1}{2}$-$\frac{7}{3}$≥x-$\frac{5+2x}{3}$,并且关于x的函数y=2|x-a|+a2的最小值为4,求常数a的值.分析 首先得出x的取值范围,再利用当x=a时,当x>a时分别得出答案.
解答 解:$\frac{3x-1}{2}$-$\frac{7}{3}$≥x-$\frac{5+2x}{3}$,
解得:x≥1,
当x=a时,y最小=a2=4,
解得:a=±2,
∵x≥1,
∴a=2,
当x>a时,y=2x+a2-2a,
∴当x=1时,
y最小=2+a2-2a=4,
解得:a=$\frac{2±2\sqrt{3}}{2}$=1±$\sqrt{3}$,
∵x≥a,
∴x≤1,
∴a=1-$\sqrt{3}$,
∴x<a时,y=-2(x-a)+a2=-2x+a2+2a无最小值,
综上所述:a=2或a=1-$\sqrt{3}$时,y=2|x-a|+a2的最小值为4.
点评 此题主要考查了一次函数与不等式,正确分类讨论是解题关键.

练习册系列答案
相关题目
9.尺规作图是指( )
| A. | 用直尺和圆规作图 | B. | 用直尺规范作图 | ||
| C. | 用刻度尺和圆规作图 | D. | 用没有刻度的直尺和圆规作图 |
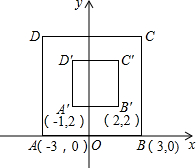 如图,在平面直角坐标xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每一个点的横,纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A、B的对应点分别为A′、B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,则点F的坐标为(1,4).
如图,在平面直角坐标xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每一个点的横,纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A、B的对应点分别为A′、B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,则点F的坐标为(1,4).