题目内容
已知:x=
,y=
,求:①x2y+xy2;②
+
的值.
| ||
|
| ||
|
| x |
| y |
| y |
| x |
考点:二次根式的化简求值
专题:
分析:首先对x、y的值分母有理化,容易求得x+y和xy的值,把所求的式子利用x+y和xy表示,代入求解即可.
解答:解:x=
=-(
+2)2=-7-4
,
y=
=-(
-2)2=-7+4
.
①原式=xy(x+y)=(-7-4
)(-7+4
)×(-14)=-14;
②原式=
=
=195.
| ||
|
| 3 |
| 3 |
y=
| ||
|
| 3 |
| 3 |
①原式=xy(x+y)=(-7-4
| 3 |
| 3 |
②原式=
| (x+y)2-xy |
| xy |
| (-14)2-1 |
| 1 |
点评:本题考查了二次根式的化简求值,正确把所求的式子利用x+y和xy表示是关键.

练习册系列答案
相关题目

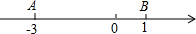 已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1,
已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1,