题目内容
3.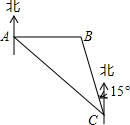 如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.
如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.(1)若台风中心不改变方向,则经过多长时间台风中心在A市正东方向的B处?(时间精确到0.1h,$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
(2)台风中心距离A市最近是多少km?
分析 (1)作BD⊥AC于D,设BD为xkm,根据方向角、利用三角函数的定义分别求出AD、DC,列出方程,解方程即可;
(2)根据正弦的定义解答即可.
解答 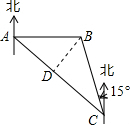 解:(1)作BD⊥AC于D,
解:(1)作BD⊥AC于D,
设BD为xkm,
由题意得,∠BAD=45°,∠ACB=30°,
则AD=x,BC=2x,CD=$\sqrt{3}$x,
∵AD+DC=AC=300,
∴x+$\sqrt{3}$x=300,
解得,x=150$\sqrt{3}$-150,
2x=300$\sqrt{3}$-300,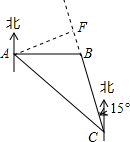
则台风中心在A市正东方向的B处需要的时间为2(150$\sqrt{3}$-150)÷50=6$\sqrt{3}$-6≈4.4h,
答:台风中心在A市正东方向的B处需要4.4h;
(2)作AF⊥CB交CB的延长线于F,
∵AC=300km,∠ACB=30°,
∴AF=$\frac{1}{2}$AC=150km.
答:台风中心距离A市最近是150km.
点评 本题考查的是解直角三角形的应用-方向角问题,正确理解方向角、熟记锐角三角函数的定义、正确作出辅助线是解题的关键》

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,双曲线y=$\frac{k}{x}$(x>0)经过点A与点B,且点A和点B的横坐标分别为a和2a(a>0),若△AOB的面积为3,则k=4.
如图,双曲线y=$\frac{k}{x}$(x>0)经过点A与点B,且点A和点B的横坐标分别为a和2a(a>0),若△AOB的面积为3,则k=4.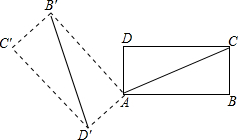 如图,在矩形ABCD中AB=3,BC=$\sqrt{3}$,若矩形ABCD绕点A逆时针旋转2∠DAC得到矩形AB′C′D′,则矩形ABCD在旋转过程中所扫过的图形的面积为4π.
如图,在矩形ABCD中AB=3,BC=$\sqrt{3}$,若矩形ABCD绕点A逆时针旋转2∠DAC得到矩形AB′C′D′,则矩形ABCD在旋转过程中所扫过的图形的面积为4π.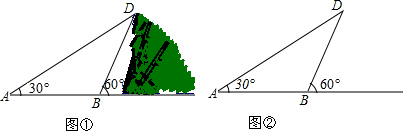
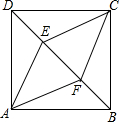 如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF,若BF=2,tan∠DAE=$\frac{1}{2}$,求四边形AECF的周长.
如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF,若BF=2,tan∠DAE=$\frac{1}{2}$,求四边形AECF的周长.