题目内容
14.已知关于x,y的方程组$\left\{\begin{array}{l}{2x+y=5m+4}\\{x-2y=-17}\end{array}\right.$.(1)求方程组的解;
(2)若方程组的解满足条件x<0,且y<0,求m的取值范围.
分析 (1)①×2+②得出5x=10m-9,求出x=2m-1.8,把x=2m-1.8代入②得出2m-1.8-2y=-17,求出y即可.
(2)根据已知和方程组的解得出不等式组,求出不等式组的解集即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=5m+4①}\\{x-2y=-17②}\end{array}\right.$,
①×2+②得:5x=10m-9,
解得:x=2m-1.8,
把x=2m-1.8代入②得:2m-1.8-2y=-17,
解得:y=m+7.6,
即方程组的解是$\left\{\begin{array}{l}{x=2m-1.8}\\{y=m+7.6}\end{array}\right.$;
(2)根据题意,得$\left\{\begin{array}{l}{2m-1.8<0}\\{m+7.6<0}\end{array}\right.$,
解得:m<-7.6,
即m的取值范围是m<-7.6.
点评 本题考查了二元一次方程组的解,解二元一次方程组,解一元一次不等式组的应用,解此题的关键是能根据题意得出一个关于m的一元一次不等式组.

练习册系列答案
相关题目
6.分式方程$\frac{2}{x-2}$=1的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=0 |
 在?ABCD中,已知∠A=25°,将△BDA沿BD翻折至△BDA′,连接CA′,∠DA′C=55°,则∠ABD=30°.
在?ABCD中,已知∠A=25°,将△BDA沿BD翻折至△BDA′,连接CA′,∠DA′C=55°,则∠ABD=30°.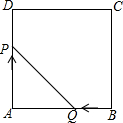 如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )
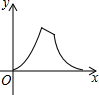
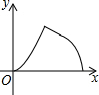
如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )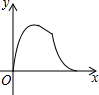

 如图.某大街水平地画有两路灯灯秆AB=CD=10米,小明晚上站在两灯杆的正中位置观察眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知底面到小明眼睛处的高度EF=1.5米;
如图.某大街水平地画有两路灯灯秆AB=CD=10米,小明晚上站在两灯杆的正中位置观察眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知底面到小明眼睛处的高度EF=1.5米;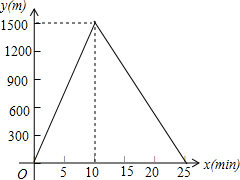 小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.
小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.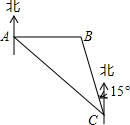 如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.
如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.