题目内容
15.为测山高,在点A处测得山顶D的仰角为30°,从点A向山的方向前进140米到达点B,在B处测得山顶D的仰角为60°(如图①).(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C(保留作图痕迹);
(2)山高DC是多少(结果保留根号形式)?
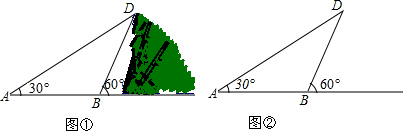
分析 (1)首先以点D为圆心,画弧交AB于两点,再分别以这两点为圆心,画弧,两弧交于一点,连接D与交点,即可求得作出垂线;
(2)由在点A处测得山顶D的仰角为30°,可求得△ABD是等腰三角形,求得BD的长,继而求得答案.
解答  解(1)如图所作DC为所求:
解(1)如图所作DC为所求:
(2)∵∠DBC=60°,∠DAB=30°,
∴∠BDA=∠DAB=30°,
∴DB=AB=140(米),
在Rt△DCB中,∠C=90°,sin∠DBC=$\frac{DC}{DB}$,
∴DC=140•sin60°=70$\sqrt{3}$(米).
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
6.分式方程$\frac{2}{x-2}$=1的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=0 |
20.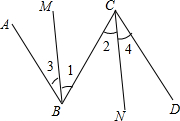 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )| A. | ∠1=∠2 | B. | ∠1=∠3且∠2=∠4 | ||
| C. | BM∥CN | D. | ∠1与∠2互补且不相等 |
 在?ABCD中,已知∠A=25°,将△BDA沿BD翻折至△BDA′,连接CA′,∠DA′C=55°,则∠ABD=30°.
在?ABCD中,已知∠A=25°,将△BDA沿BD翻折至△BDA′,连接CA′,∠DA′C=55°,则∠ABD=30°.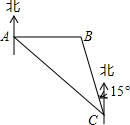 如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.
如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动. 如图所示,在△ABC中,在△ACB=90°,CD平分△ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.
如图所示,在△ABC中,在△ACB=90°,CD平分△ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.