题目内容
12.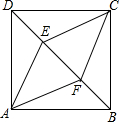 如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF,若BF=2,tan∠DAE=$\frac{1}{2}$,求四边形AECF的周长.
如图,正方形ABCD中,点E、F为对角线BD上两点,DE=BF,若BF=2,tan∠DAE=$\frac{1}{2}$,求四边形AECF的周长.
分析 如图,连接AC交BD于点O.,作EM⊥AD于M,先证明四边形AECF是菱形,在RT△AME中,求出AM、EM即可解决问题.
解答 解:如图,连接AC交BD于点O.,作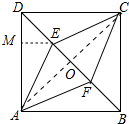 EM⊥AD于M.
EM⊥AD于M.
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD,∠ADB=45°
∵DE=BF,
∴OE=OF,OA=OC,
∴四边形AECF是平行四边形,∵EF⊥AC,
∴四边形AECF是菱形,
∴AE=EC=CF=AF,
在RT△DME中,∵∠DME=90°,∠MDE=45°,DE=BF=2,
∴DM=ME=$\sqrt{2}$,
∵tan∠EAM=$\frac{1}{2}$=$\frac{EM}{AM}$,
∴AM=2EM=2$\sqrt{2}$,
∴AE=$\sqrt{A{M}^{2}+E{M}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=$\sqrt{10}$,
∴四边形AECF的周长=4AE=4$\sqrt{10}$.
点评 本题考查正方形的性质、菱形的判定和性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
20.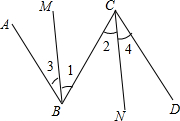 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )| A. | ∠1=∠2 | B. | ∠1=∠3且∠2=∠4 | ||
| C. | BM∥CN | D. | ∠1与∠2互补且不相等 |
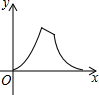
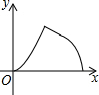
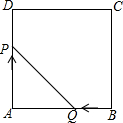 如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )
如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )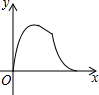

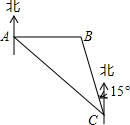 如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.
如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动. 如图所示,在△ABC中,在△ACB=90°,CD平分△ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.
如图所示,在△ABC中,在△ACB=90°,CD平分△ACB,DE⊥AC于E,DF⊥BC于F,求证:四边形CEDF是正方形.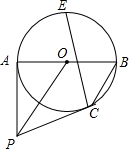 如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.