题目内容
11.解方程(组):(1)$\left\{\begin{array}{l}{x-y=3}\\{2y+3(x-y)=11}\end{array}\right.$
(2)$\frac{2}{1-x}$+1=$\frac{x}{1+x}$
(3)$\left\{\begin{array}{l}{2x+3y-z=3}\\{3x-2y+z=4}\\{x+2y+z=10}\end{array}\right.$.
分析 (1)将x-y看作整体,用代入消元法求解可得;
(2)方程两边都乘以(1+x)(1-x)化分式方程为整式方程,解整式方程可得x的值,检验可得;
(3)用加减消元法求解可得.
解答 解:(1)解方程组$\left\{\begin{array}{l}{x-y=3}&{①}\\{2y+3(x-y)=11}&{②}\end{array}\right.$,
将①代入②,得:2y+9=11,解得:y=1,
将y=1代入①得:x-1=3,解得:x=4,
故方程组的解为:$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$;
(2)方程两边都乘以(1+x)(1-x)得:2(1+x)+(1+x)(1-x)=x(1-x),
解得:x=-3,
经检验x=-3是原分式方程的解,
故原分式方程的解为x=-3;
(3)解方程组$\left\{\begin{array}{l}{2x+3y-z=3}&{①}\\{3x-2y+z=4}&{②}\\{x+2y+z=10}&{③}\end{array}\right.$,
①+②,得:5x+y=7 ④,
①+③,得:3x+5y=13 ⑤,
④×5-⑤,得:22x=22,解得:x=1,
将x=1代入④,得:5+y=7,解得:y=2,
将x=1、y=2代入①,得:2+6-z=3,解得:z=5,
故方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=5}\end{array}\right.$
点评 本题主要考查解方程组、解分式方程的能力,熟练掌握解方程的两种方法和解分式方程的转化思想是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.分式方程$\frac{2}{x-2}$=1的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=0 |
20.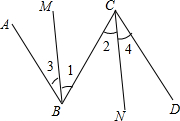 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )| A. | ∠1=∠2 | B. | ∠1=∠3且∠2=∠4 | ||
| C. | BM∥CN | D. | ∠1与∠2互补且不相等 |
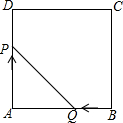 如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )
如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )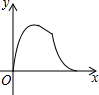

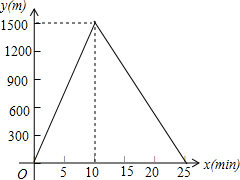 小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.
小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.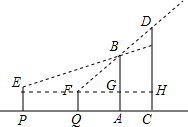 如图,两棵人树AB、CD,它们根部的距离AC=4m.小强沿着正对这两棵树的方向前进,如果小强的眼睛与地面的距离为1.6m,小强在P处时测得B的仰角为20.3°,当小强前进5m达到Q处时,视线恰好经过两棵树的顶部B和D,此时仰角为36.42°.
如图,两棵人树AB、CD,它们根部的距离AC=4m.小强沿着正对这两棵树的方向前进,如果小强的眼睛与地面的距离为1.6m,小强在P处时测得B的仰角为20.3°,当小强前进5m达到Q处时,视线恰好经过两棵树的顶部B和D,此时仰角为36.42°.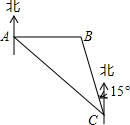 如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.
如图,沿海城市A测得台风中心在东南方向300km的C处,并以50km/h的速度沿北偏西15°的方向移动.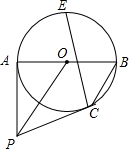 如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.